В каждом вычислительном эксперименте время окончания счета
равнялось
t
к
= 80
, а шаг
Δ
t
= 0
,
04
, т.е. проводилось 2000 шагов рас-
чета. Нестационарные коэффициенты сопротивления осреднялись по
1500 временных шагов (на интервале от 500-го до 2000-го шага). По-
лученные таким образом стационарные коэффициенты сопротивления
сравнивались с экспериментальными данными [9].
На первом этапе исследований выбирали безразмерные параметры
расчетной схемы. В качестве тестового объекта был выбран тонкий
диск диаметром
D
= 1
и толщиной
H
= 0
,
1
. В диапазоне чисел Рей-
нольдса Re от 10
3
до 10
7
стационарный коэффициент сопротивления
для характерной площади
S
= 0
,
25
πD
2
имеет постоянное значение
C
exp
X
= 1
,
17
[9].
По результатам вычислительных экспериментов были выбраны
безразмерные параметры
V
∞
=
{
1
,
0
,
0
}
т
;
ρ
∞
= 1
;
p
∞
= 1
;
β
= 0
,
01
;
ε
= 0
,
1
;
ε
∗
= 0
,
7
ε
;
ε
∗∗
= 0
,
9
;
ε
Δ
= 0
,
02
;
Γ
min
= 10
−
6
;
L
far
= 10
,
0
.
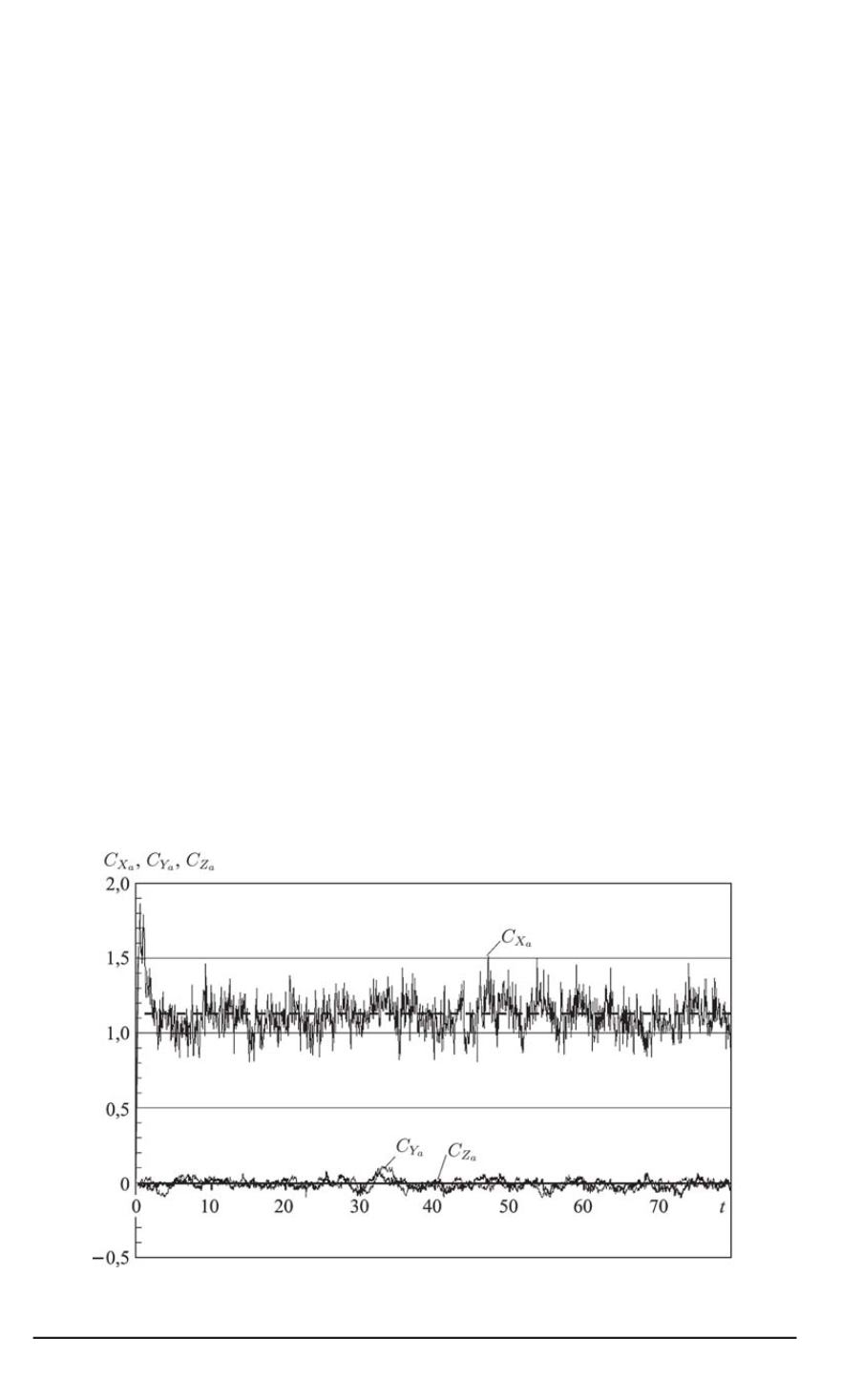
В качестве примера на рис. 3 приведена зависимость изменения
коэффициентов
C
X
a
, C
Y
a
, C
Z
a
от времени для диска с параметрами
N
1
= 22
,
N
2
= 36
. На рис. 4 показан вид вихревого следа, сформиро-
ванного
N
= 8667
ВЭ (отмечены на рисунке точками), на последнем
шаге расчета (
t
= 80)
.
В таблице приведены значения стационарного коэффициента со-
противления диска, вычисленного для различных значений параме-
тров дискретизации модели. Из таблицы видно, что с увеличением
дискретизации погрешность определения коэффициента сопротивле-
ния уменьшается.
На втором этапе исследований, используя определенные ранее без-
размерные параметры, проводили моделирование обтекания шара.
Рис. 3. Зависимость коэффициентов
C
X
a
,
C
Y
a
,
C
Z
a
от времени для диска
(штриховая — экспериментальное значение)
32 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 2


