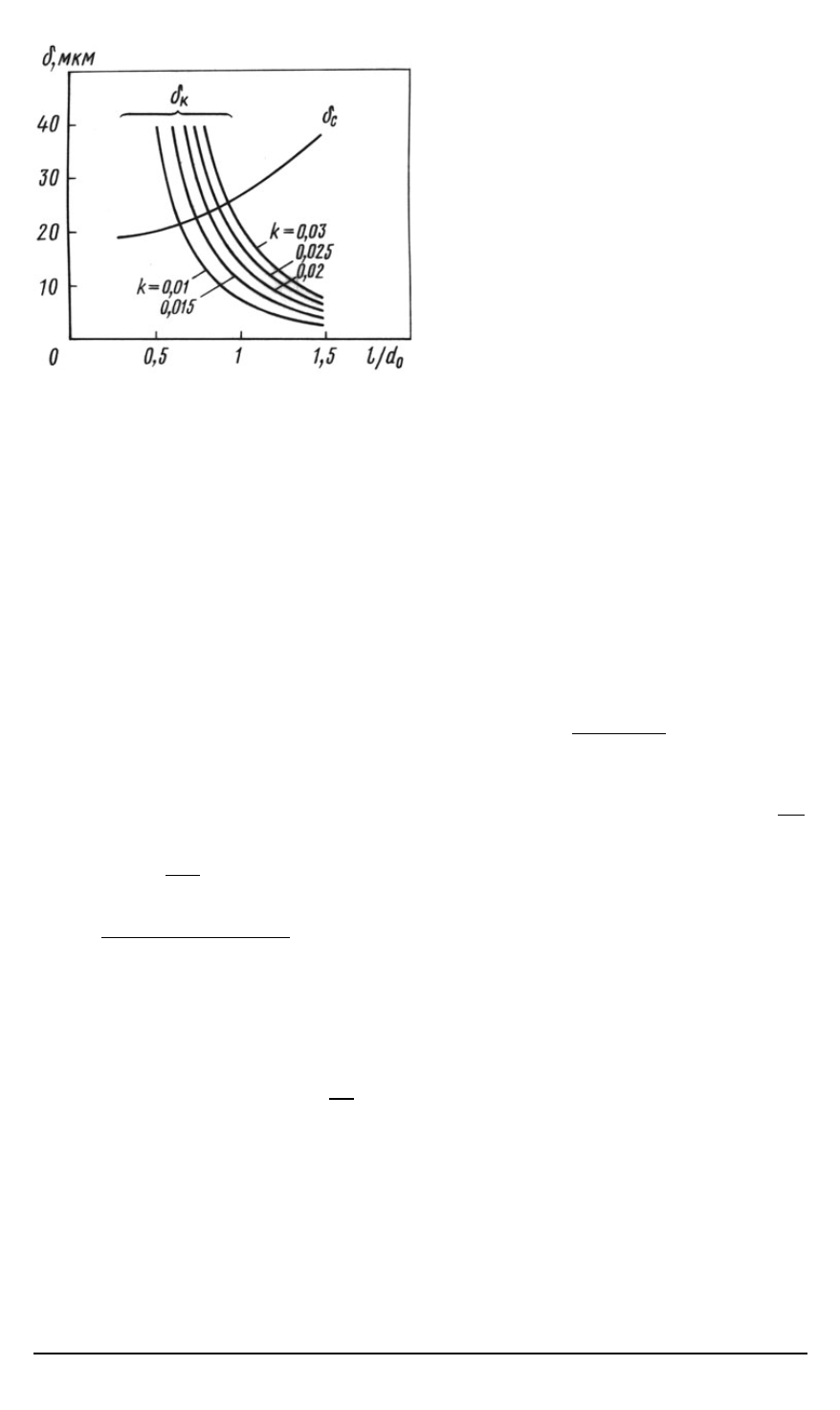
Рис. 4. Графики зависимости податливо-
сти
δδ
от соотношения межопорной дли-
ны
l
к диаметру оправки
d
0
Проанализировав уравнения
(3) и (4), выявили, что при изме-
нении длины
l
меняются значе-
ния контактных и собственных
податливостей. Причем при уве-
личении
l
контактная податли-
вость уменьшается, а собствен-
ная увеличивается, что нагляд-
но видно из графиков на рис. 4
(
D
= 63
мм и
L
= 100
мм). Это
можно объяснить уменьшением
реакций
Y
A
и
Y
B
опор при уве-
личении межопорной длины
l
.
Из приведенных графиков сле-
дует, что условие
δ
к
+
δ
c
=
δ
min
соблюдается или в точке их пересечения при
δ
c
=
δ
к
, или в ее окрест-
ностях.
Разработанный алгоритм (рис. 5) позволяет быстро и с достаточной
точностью найти оптимальное соотношение
l/d
для каждого значения
контактной податливости
δ
и ее коэффициента
k
,
l
опт
= 1
,
2
. . .
1
,
5
d
.
Исходные данные для оптимизации:
D
= 32
,
40
,
50
,
63
,
80
,
100
мм;
Р
= 100
дан;
L
= 100
мм;
d
0
= 0
,
57
D
;
d
1
= 1
,
15
d
0
;
α
= 8
◦
17
;
E
= 2
,
1
·
10
5
МПа;
k
= 0
,
1; 0
,
15; 0
,
2; 0
,
25; 0
,
3
,
мкм
Н
·
мм
−
2
.
Жесткость
j
торцевого соединения (см. рис. 1) можно определить
по известным зависимостям
1
плоских кольцевых стыков:
j
т
=
М
ϕ
или
j
т
=
P
ϕL
, где
М
=
PL
, Н
·
м;
ϕ
— угол поворота в стыке,
ϕ
=
k
(1
−
χ
)
M
·
10
−
3
I
, мкм/мм,
k
— коэффициент контактной по-
датливости определяется по формуле (1);
χ
— величина, учитывающая
податливость затяжных элементов, для винтов
1
χ
= 0
,
1
. . .
0
,
2
,
I
—
момент инерции кольцевого стыка,
I
=
π
64
D
4
−
d
4
,
мм
4
.
Рассматривая зависимости по определению жесткости кольцевого
стыка, можно для постоянного наружного диаметра
D
аналитически
определить внутренний диаметр
d
, зависящий от типоразмера инстру-
ментальной системы, при котором жесткость соединения будет мак-
симальная, т.е. оптимизировать соотношение
d/D
для всех систем по
критерию максимальной жесткости. Согласно приведенным зависимо-
30 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2005. № 4


