ϕ
(
ρ,
Fo) =
L
−
1
[Φ(
ρ, s
)]
≡
≡
2
π
∞
Z
0
exp(
−
s
2
Fo)
α
(
s
)
Y
0
(
ρs
)
−
β
(
s
)
J
0
(
ρs
)
α
2
(
s
) +
β
2
(
s
)
ds, ρ
≥
1
,
Fo
≥
0
,
(12)
где
α
(
s
) =
J
1
(
s
)
−
εsJ
0
(
s
);
(13)
β
(
s
) =
Y
1
(
s
)
−
εsY
0
(
s
)
.
Воспользовавшись результатами проведенных исследований
,
по
-
дробнее проанализируем особенности процесса формирования темпе
-
ратурного поля в неограниченном твердом теле с термически тонким
теплоактивным стержневым элементом при
Q
(Fo) =
Q
0
=
const.
В
этом случае
,
согласно уравнениям
(11)
и
(12),
температурное поле в
твердом теле определяется как
Θ(
ρ,
Fo) =
2
Q
0
π
∞
Z
0
1
−
e
−
s
2
Fo
s
2
α
(
s
)
Y
0
(
ρs
)
−
β
(
s
)
J
0
(
ρs
)
α
2
(
s
) +
β
2
(
s
)
ds,
ρ
≥
1
,
Fo
≥
0
,
(14)
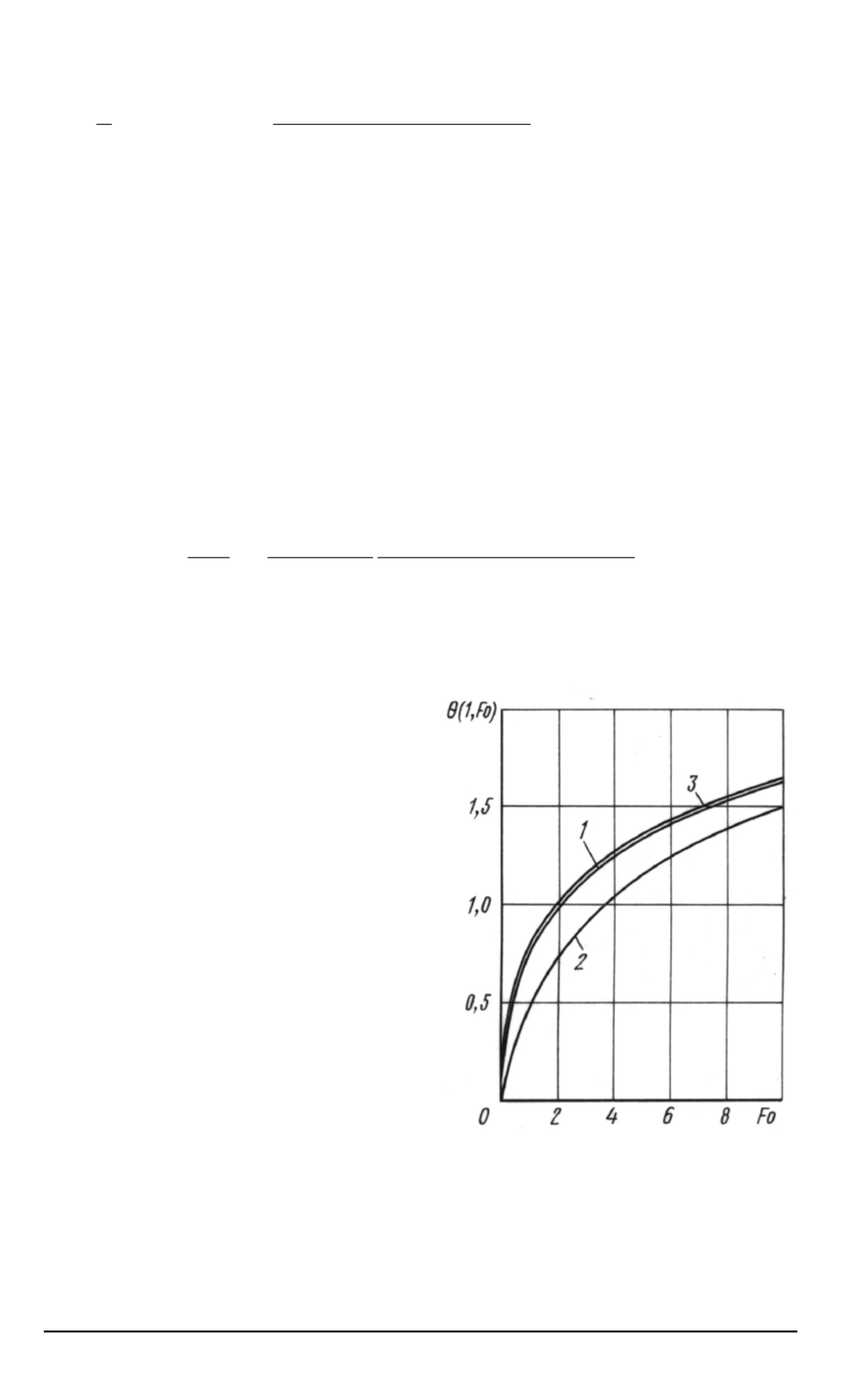
Рис
. 3.
Зависимость безразмерной
температуры поверхности твердо
-
го тела
,
содержащего термически
тонкий теплоактивный стержневой
элемент
,
от времени при различных
значениях параметра
ε
:
1
— 0,1;
2
— 1,0;
3
— 0
где функции
α
(
s
)
и
β
(
s
)
задают
-
ся равенствами
(13).
При
ε
= 0
интегральное представление
(14)
для функции
Θ(
ρ,
Fo)
преобразует
-
ся к полученному в работах
[1, 3].
Температуру граничной поверхно
-
сти твердого тела можно опреде
-
лить из равенства
(14)
при
ρ
= 1
.
Заметим
,
что для практики значе
-
ние этой температуры представля
-
ет наибольший интерес
,
посколь
-
ку позволяет оценить величину
предельно достижимого разогре
-
ва твердого тела
,
подверженного
тепловому воздействию
.
На рис
. 3
приведены результаты
расчетов температурного профиля
Θ(1
,
Fo)
поверхности
ρ
= 1
твердо
-
го тела с теплоактивным термиче
-
ски тонким стержневым элементом
при воздействии теплового потока
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
1 29


