Φ(
ρ, s
) =
K
0
(
ρ
√
s
)
√
s
[
ε
√
sK
0
(
√
s
) +
K
1
(
√
s
)]
.
(9)
Для завершения процедуры решения задачи
(2)
осталось реализо
-
вать переход от изображения
U
(
ρ, s
)
,
определяемого равенствами
(8)
и
(9),
к соответствующему оригиналу
Θ(
ρ,
Fo)
с использованием форму
-
лы обращения интегрального преобразования Лапласа
[1–4]:
Θ(
ρ,
Fo) =
L
−
1
[
U
(
ρ, s
)]
≡
1
2
πi
σ
+
i
∞
Z
σ
−
i
∞
exp(
s
Fo)
U
(
ρ, s
)
ds,
где
L
−
1
[
·
]
—
оператор обращения интегрального преобразования Ла
-
пласа
,
поскольку непосредственное его обращение с использованием
таблиц
“
изображение
–
оригинал
” [2, 15]
в рассматриваемом случае не
представляется возможным
.
Для преодоления возникших трудностей
воспользуемся следующим приемом
.
Полагая
ϕ
(
ρ,
Fo) =
L
−
1
[Φ(
ρ, s
)]
, Q
(Fo) =
L
−
1
[Π(
s
)]
,
(10)
согласно теореме о свертках
[2],
находим
Θ(
ρ,
Fo) =
Fo
Z
0
Q
(Fo
−
τ
)
ϕ
(
ρ, τ
)
dτ, ρ
≥
1
,
Fo
≥
0
.
(11)
Таким образом
,
если вид зависимости
Q
=
Q
(Fo)
конкретизирован
,
то для определения температурного поля в твердом теле необходимо
лишь найти оригинал
ϕ
(
ρ,
Fo)
соответствующего изображения
Φ(
ρ, s
)
.
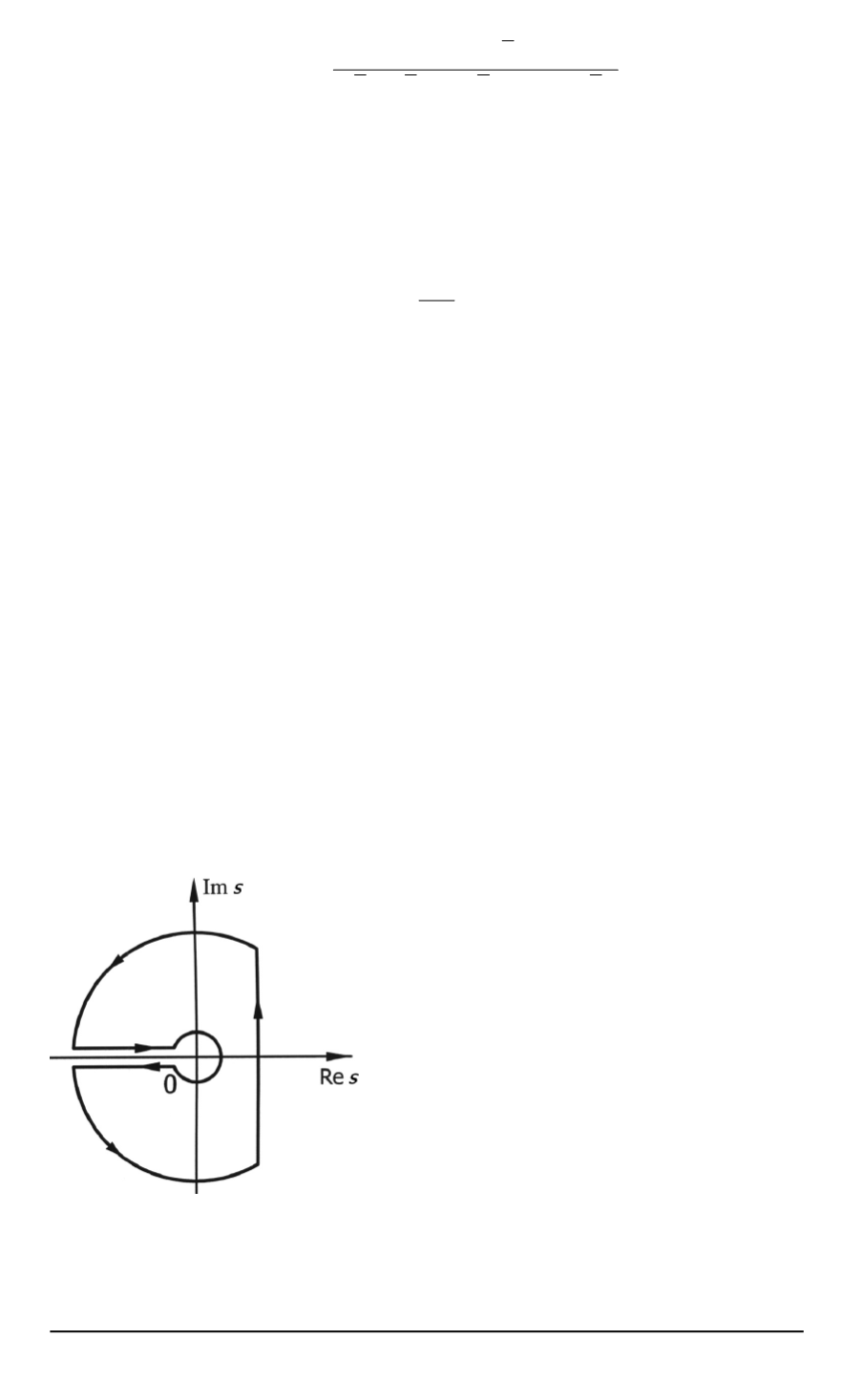
Рис
. 2.
Ориентированный контур в
комплексной плоскости
s
для вы
-
числения интеграла Меллина
Поскольку
,
согласно уравнению
(9),
изображение этого оригинала име
-
ет единственную особую точку в нача
-
ле координат комплексной плоскости
,
являющуюся точкой ветвления
,
то
,
воспользовавшись стандартной тех
-
никой вычисления интегралов Мел
-
лина
[1, 2]
и ориентированным кон
-
туром
,
приведенным на рис
. 2,
а так
-
же известными представлениями
[14]
модифицированных функций Бессе
-
ля
K
ν
(
·
)
через функции Бесселя
J
ν
(
·
)
и
Y
ν
(
·
)
индекса
ν
первого и второго
рода соответственно
,
приходим к сле
-
дующему результату
:
28 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
1


