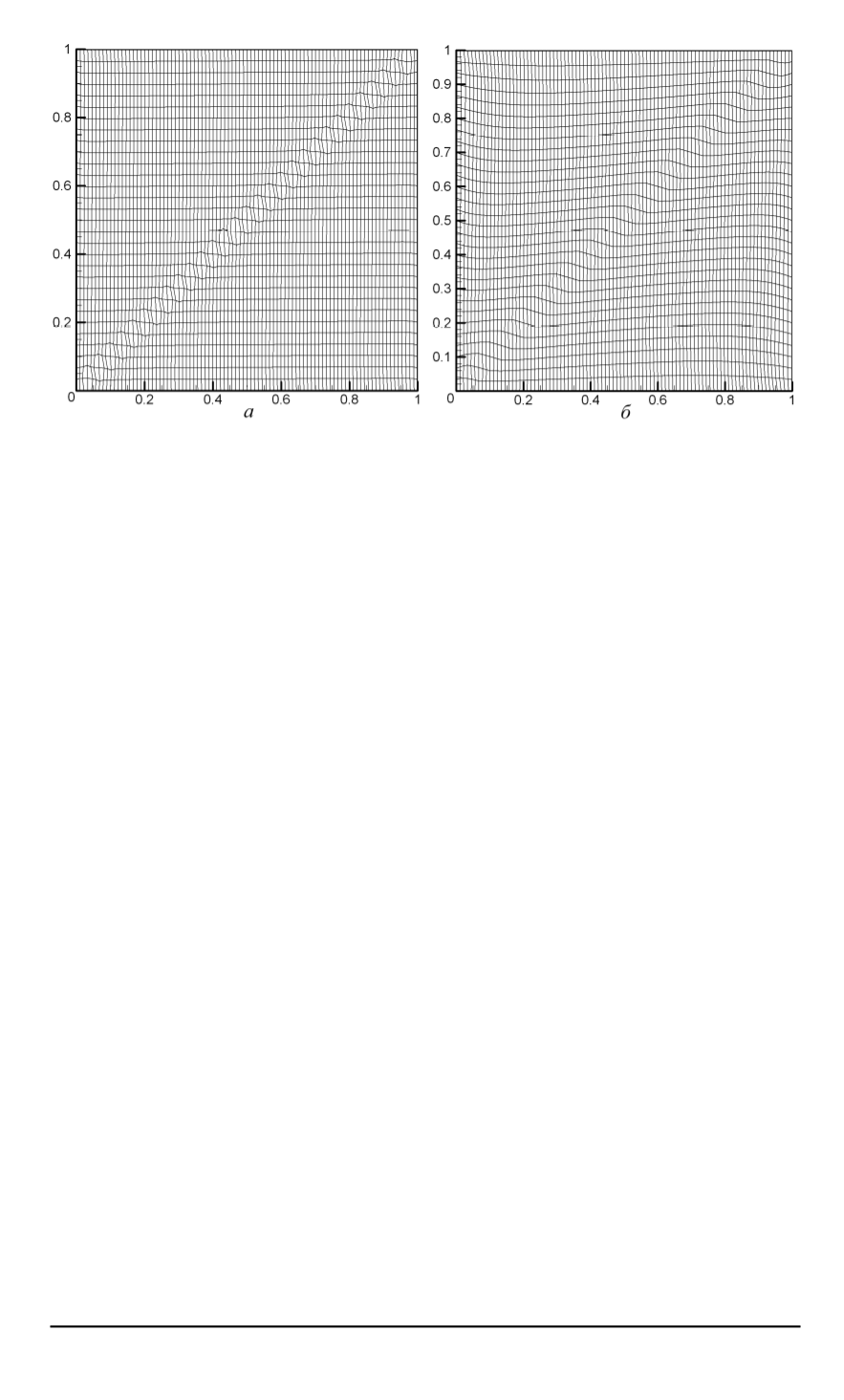
Рис. 2. Регулярная расчетная сетка, построенная с применением объемной упра-
вляющей функции
f
(
x, y
) = exp
−
A
(
x
−
y
)
2
с помощью разработанной чис-
ленной методики (
а
) и численной адаптации с использованием ортогонализи-
рующей процедуры (
б
)
где
P, Q
— параметры, обеспечивающие контроль распределения точек
сетки. Параметр
P
задает степень отличия от линейного распределе-
ния, а
Q
является “демпфирующим фактором”.
Пример 2.
В этом примере в прямоугольной области физического
пространства расчетная сетка адаптируется к функции вида
f
(
x, y
) = exp
−
A
(
x
−
y
)
2
, A
= 20
.
Этот пример, как отмечается в работе [6], моделирует достаточно
сложную ситуацию для адаптации регулярной четырехугольной сет-
ки: управляющая функция
f
имеет градиенты, образующие с границей
расчетной области угол, близкий к
45
◦
, что может приводить к сильной
скошенности адаптированной сетки.
Результаты расчетов, представленные на рис. 2,
а
, основаны на си-
стеме уравнений (1).
Расчетная сетка, полученная с помощью системы уравнений (2) и
приведенная на рис. 2,
б
, соответствует численной методике постро-
ения квазиортогональных регулярных криволинейных адаптивных
сеток.
Работа выполнена при частичной поддержке программ фунда-
ментальных исследований РАН и грантов РФФИ №05-01-00780 и
№07-01-00133.
СПИСОК ЛИТЕРАТУРЫ
1. И г н а т ь е в А. А. Построение регулярных сеток с помощью механической
аналогии // Математическое моделирование. – 2000. – Т. 12, № 2. – C. 101–105.
10 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 1


