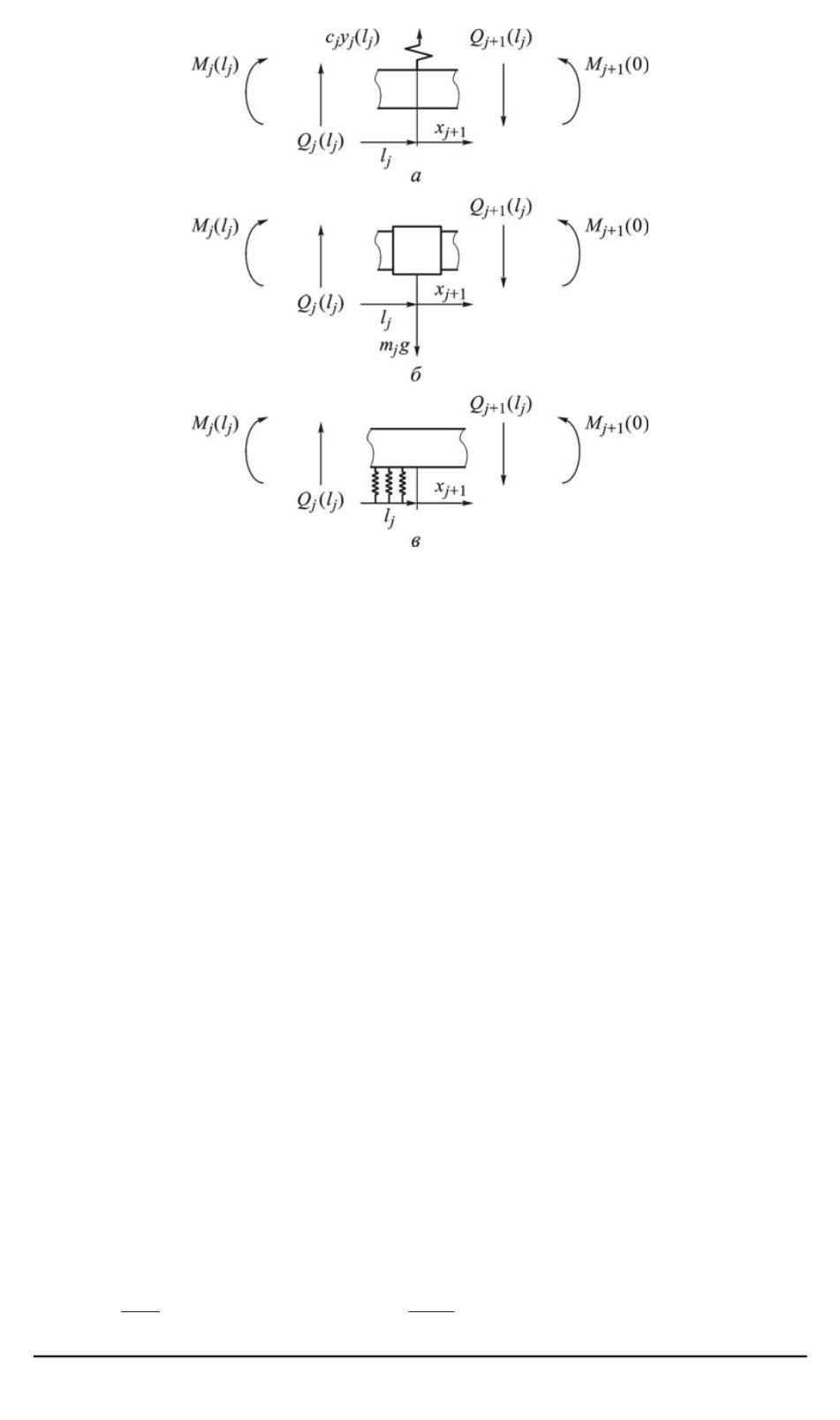
Рис. 2. Расчетные схемы стыков участков:
а
— с пружиной;
б
— с сосредоточенной массой;
в
— с упругой подушкой
где
B
j
— матрица и
b
j
— вектор перехода стыка, определяемые по
формулам
B
j
=
⎛
⎜⎜⎝
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
⎞
⎟⎟⎠
, b
j
= 0 0 0
−
m
j
g
т
.
Для стыка с упругой подушкой формула перехода будет иметь вид
X
j
+1
(0) =
B
j
X
j
(1)
.
(8)
Матрицы переходов через участки.
Решать поставленную задачу
будем методом начальных параметров [1], в соответствии с которым
векторсостояния сечения на левом конце стержня
X
1
(0)
связан с век-
тором состояния сечения на правом конце
X
N
(1)
следующим образом:
X
N
(1) =
A
1
N
(
B
N
A
N
−
1
. . .
(
A
4
(
B
4
(
A
3
B
1
3
(
A
2
B
2
(
A
1
1
X
1
(0)+
+
a
1
) +
a
2
) +
a
3
) +
b
4
) +
a
4
) +
. . .
+
a
N
.
Здесь
b
4
, b
6
, b
8
— векторы переходов через стыки с сосредоточенной
массой.
Матрицы
A
1
1
=
F
1
(1)
·
F
−
1
1
(0)
,
A
1
N
=
F
N
(1)
·
F
−
1
N
(0)
и векторы
a
1
=
μ
1
g
k
1
0 0 0
т
,
a
N
=
μ
N
g
k
N
0 0 0
т
переходов подзем-
104 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 3


