
А.В. Аттетков, П.А. Власов, И.К. Волков
92
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 5
2
0,
,
U L
(6)
где надстрочной точкой обозначена производная по переменной
Fo.
Начальное
условие при
Fo 0
в смешанной задаче (1) в автомодельных переменных (2)
будет иметь вид краевого условия задачи (4)−(6), заданного при
.
Непосредственный анализ краевой задачи (4)−(6) показывает, что исполь-
зуемая подстановка (2) приводит к автомодельному решению при выполнении
следующих условий:
0
Fo Fo
const;
(7)
0
Fo
const;
(8)
0
Fo
const,
(9)
где постоянная
0
принимает лишь неотрицательные значения, а
0
,
0
— по-
ложительные постоянные. Искомое автомодельное решение в этом случае будет
обладать тем свойством, что со временем изменяется только масштаб автомо-
дельной переменной
0,
а масштаб функции
U
остается неизменным.
Условие автомодельности (7) реализуется лишь для следующего закона
движения границы объекта исследований:
0
Fo 2 Fo.
(10)
При выполнении этого условия решение обыкновенного дифференциаль-
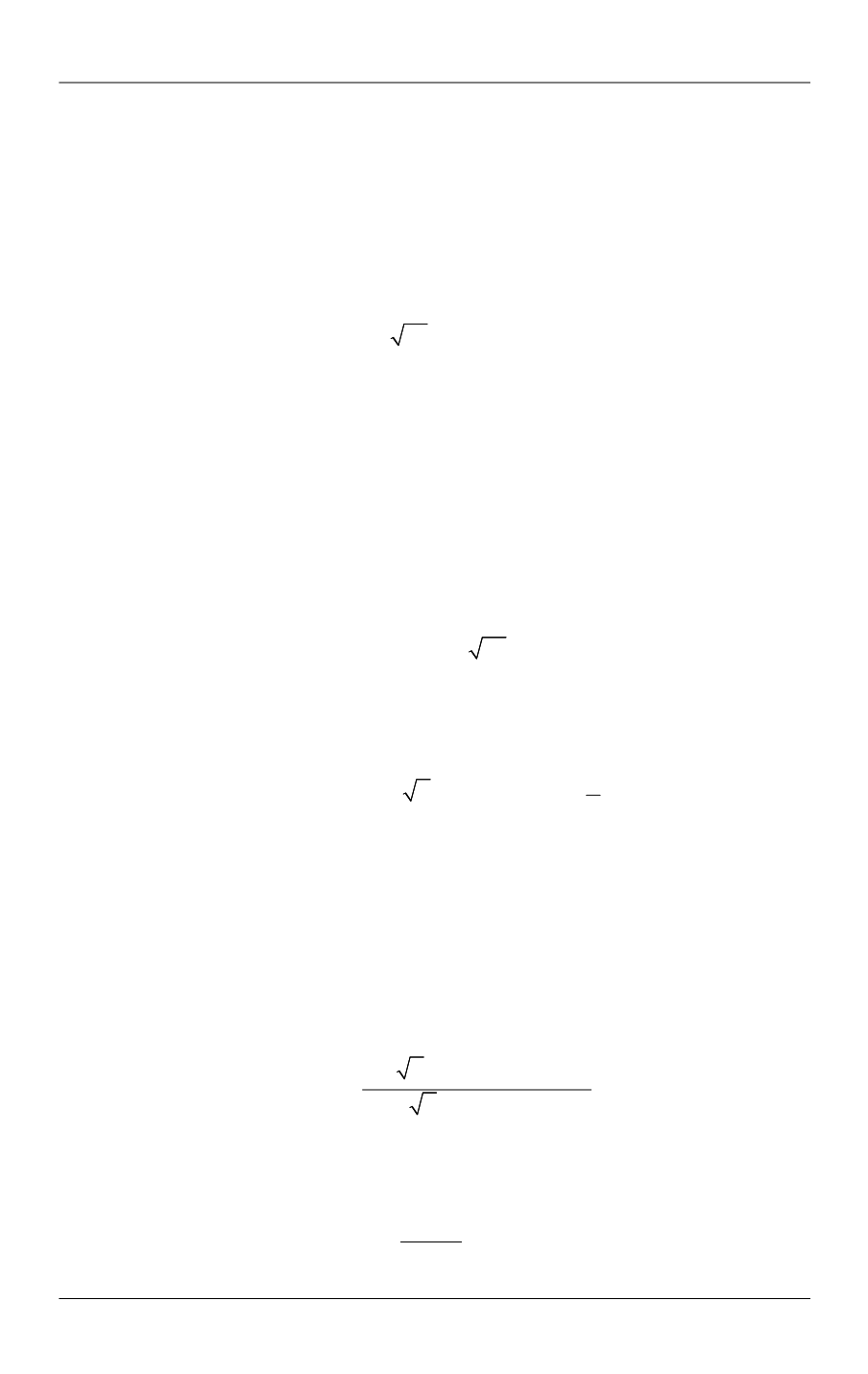
ного уравнения второго порядка (4) находится стандартными методами [18] и
имеет вид
2
0
0
0
0
0 exp
erfc
erfc
,
0,
2
U U U
(11)
где
erfc ( )
— дополнительная функция ошибок Гаусса [2]; штрихом обозначена
производная по переменной
.
Используя равенство (11), с учетом условий автомодельности (8), (9), равен-
ства (10), краевого условия (5) и условия (6) принадлежности функции
U
классу интегрируемых с квадратом функций, находим безразмерную темпера-
туру
0
U
границы изотропного полупространства в изучаемом автомодель-
ном режиме теплопереноса:
2
0
0
0
0
2
0
0
0
exp erfc
0
.
1
exp erfc
U
(12)
При этом справедлива следующая асимптотическая оценка при больших
значениях
0
:
0
0 0
0 0
0 ~
0.
U
















