
Анализ особенностей численного моделирования конвективных тепловых потоков…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 1
99
Для решения рассматриваемых задач успешно используются Reynolds —
averaged Navier — Stokes (RANS) методы, основанные на решении уравнений
Навье — Стокса, осредненных по Рейнольдсу или Фавру и дополненных урав-
нениями турбулентного переноса. Данные методы позволяют оптимизировать
вычислительные ресурсы машинного времени и, в случае надлежащего выбора
математической модели, а также параметров конечно-объемной расчетной об-
ласти, обеспечить удовлетворительное совпадение расчетов с экспериментом.
В частности, для достижения требуемой точности необходимо использовать
наиболее подходящие модели турбулентности и обеспечить определенные зна-
чения безразмерной толщины пристеночной ячейки
y
+
. Существующие реко-
мендации по выбору параметра
y
+
[1, 2] имеют приближенный характер, и для
каждого конкретного случая требуется их уточнение.
Одно из возможных уравнений для определения значения параметра
y
+
следующее:
тр
+
ρ
,
μ
v y
y
где
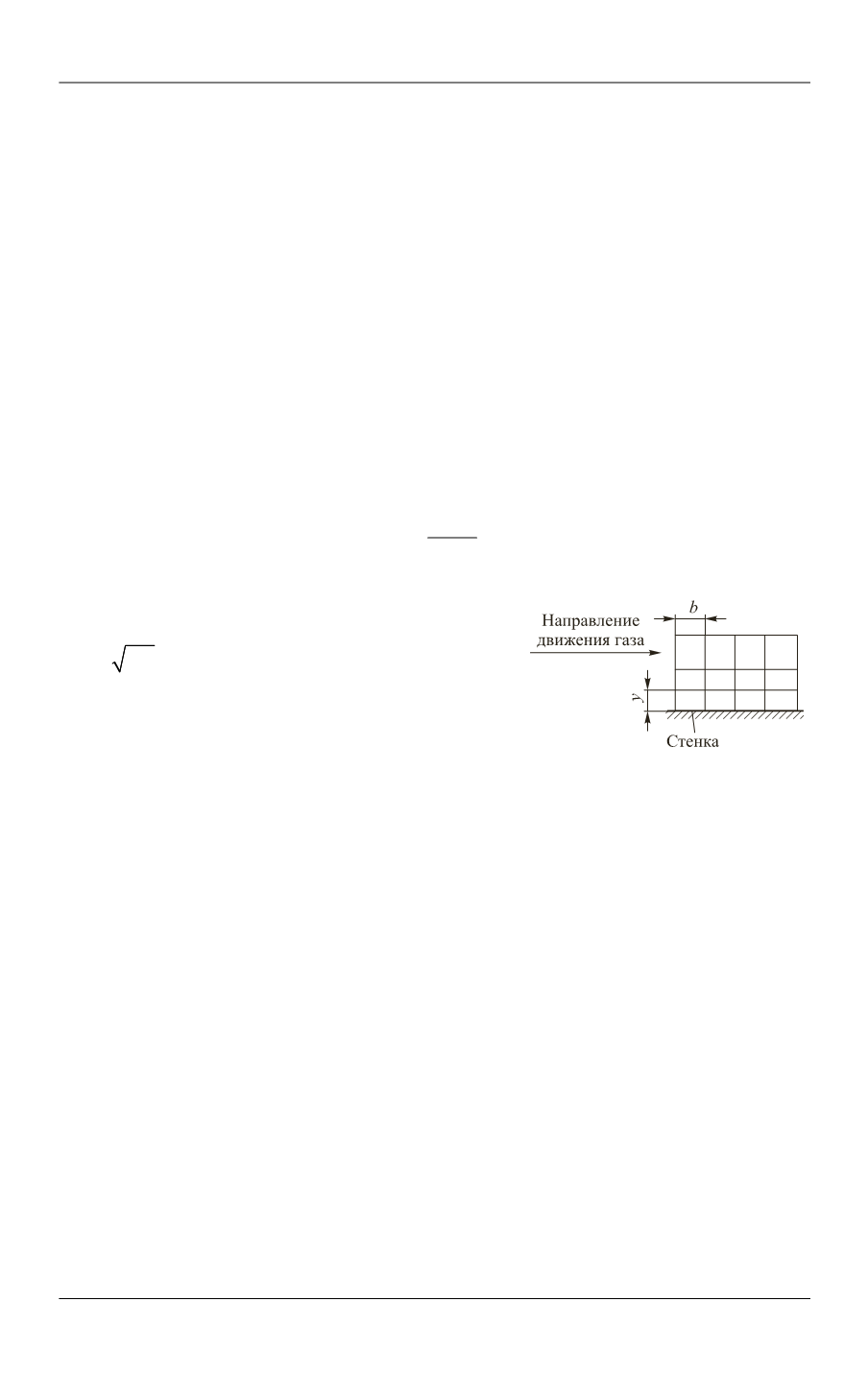
y
— толщина пристеночной ячейки; ρ —
плотность газа; μ — динамическая вязкость газа;
тр
τ/ρ
v
— скорость трения, τ — касательные
напряжения, рассчитанные в пристеночной
ячейке (рис. 1).
Рекомендации по выбору значения пара-
метра
y
+
обычно имеют своей целью достижение
рационального баланса в решении двух базовых
задач: получение адекватных параметров погра-
ничного слоя (ПС) и оптимизация времени расчета. Под адекватными парамет-
рами ПС будем понимать параметры, соответствующие экспериментальным
данным, что является определяющим в рассмотрении конвективного теплового
потока от газа к стенке.
Существует два подхода к моделированию пристеночной области течения.
Первый подход подразумевает использование полуэмпирических зависимостей,
описывающих профиль пограничного слоя без разрешения вязкостного и пере-
ходного подслоев. Данные зависимости именуются «пристеночными функция-
ми» и используются для описания области, заключенной между стенкой и обла-
стью полностью турбулентного потока. Второй подход подразумевает разреше-
ние вязкостного и переходного подслоев вследствие сгущения расчетной сетки
в пристеночной области.
Основное преимущество первого подхода — меньшее число ячеек расчет-
ной сетки для описания пристеночной области. Однако использование первого
подхода может привести к результатам, не соответствующим эксперименталь-
Рис. 1.
Фрагмент расчетной
сетки
















