Вводя обозначение
q
=
−
4
b
a
Y
, получаем выражение для интеграла
Z
ndt
в виде
Z
ndt
=
q
γY
1
1
−
exp(
γ t
)
∙
Y
+
C
1
.
Тогда
T
=
Kq
γY
1
1
−
exp(
γ t
)
∙
Y
+
C
2
.
При
t
= 0
и
T
= 0
С
2
=
−
Kq
γY
1
1
−
Y
и значение изменения темпера-
туры
Т
будет
T
=
Kq
γY
1
1
−
exp(
γ t
)
∙
Y
−
1
1
−
Y
.
(12)
Текущее значение реактивности определяется как
ρ
=
ρ
0
−
αT
и тогда
ρ
=
ρ
0
−
αKq
γY
1
1
−
exp(
γ t
)
∙
Y
−
1
1
−
Y
.
(13)
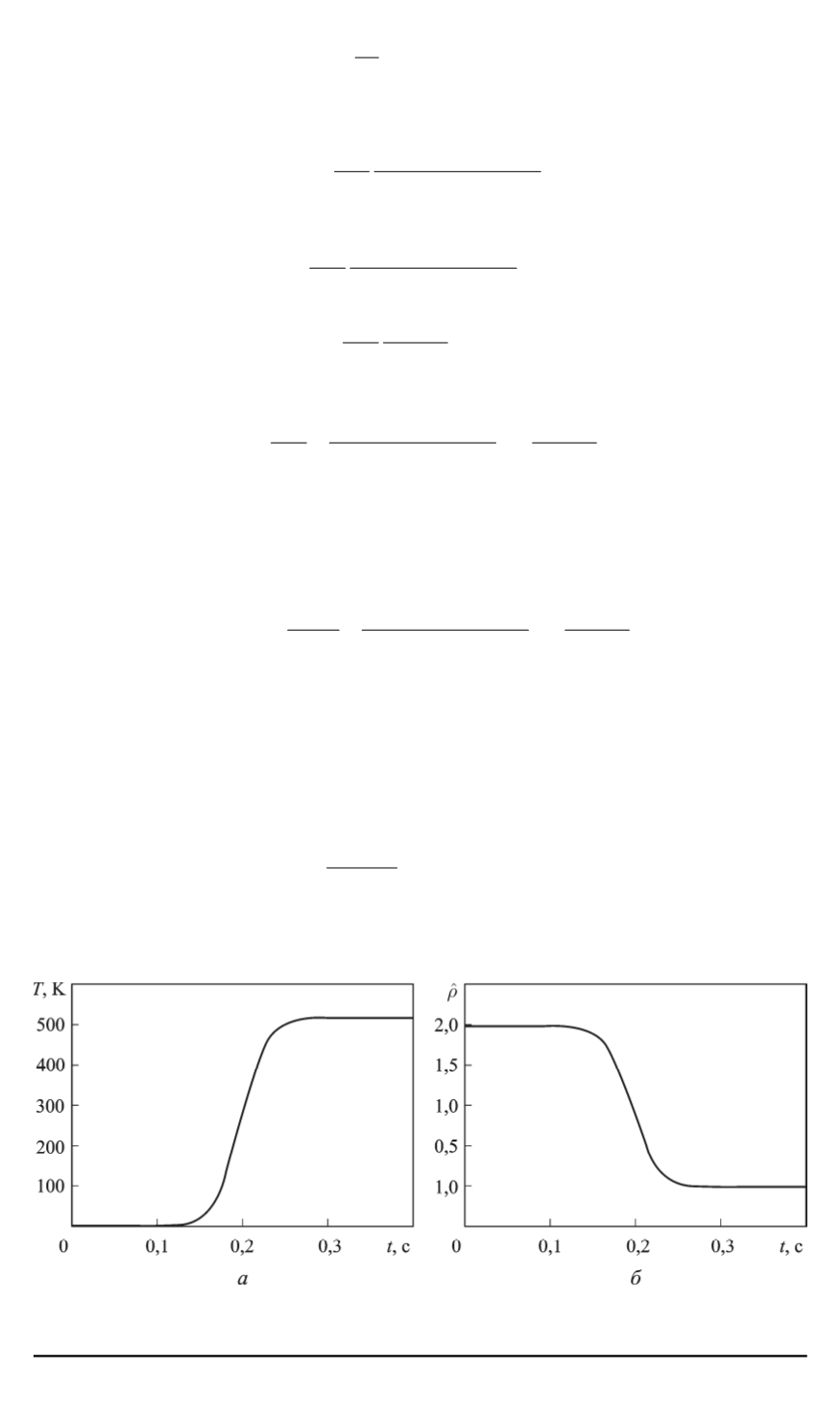
На рис. 4 приведены рассчитанные по формулам (12) и (13) за-
висимости. Следует еще раз подчеркнуть их полную идентичность
численным решениям модели Нордгейма–Фукса (2). При этом значе-
ния
Т
и
ρ
по окончании быстрого импульса полностью соответствуют
значениям, получаемым из модели Нордгейма-Фукса:
T
= 2
ρ
0
−
β
α
и
ρ
= 2
β
−
ρ
0
.
Естественно, что полученные аналитические решения справедли-
вы только во время быстрого импульса и неприменимы, как и сама
Рис. 4. Изменение отклонения температуры (
а
) и реактивности (
б
) в быстром
импульсе при
ˆ
ρ
0
= 2
β
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2013. № 3 9


