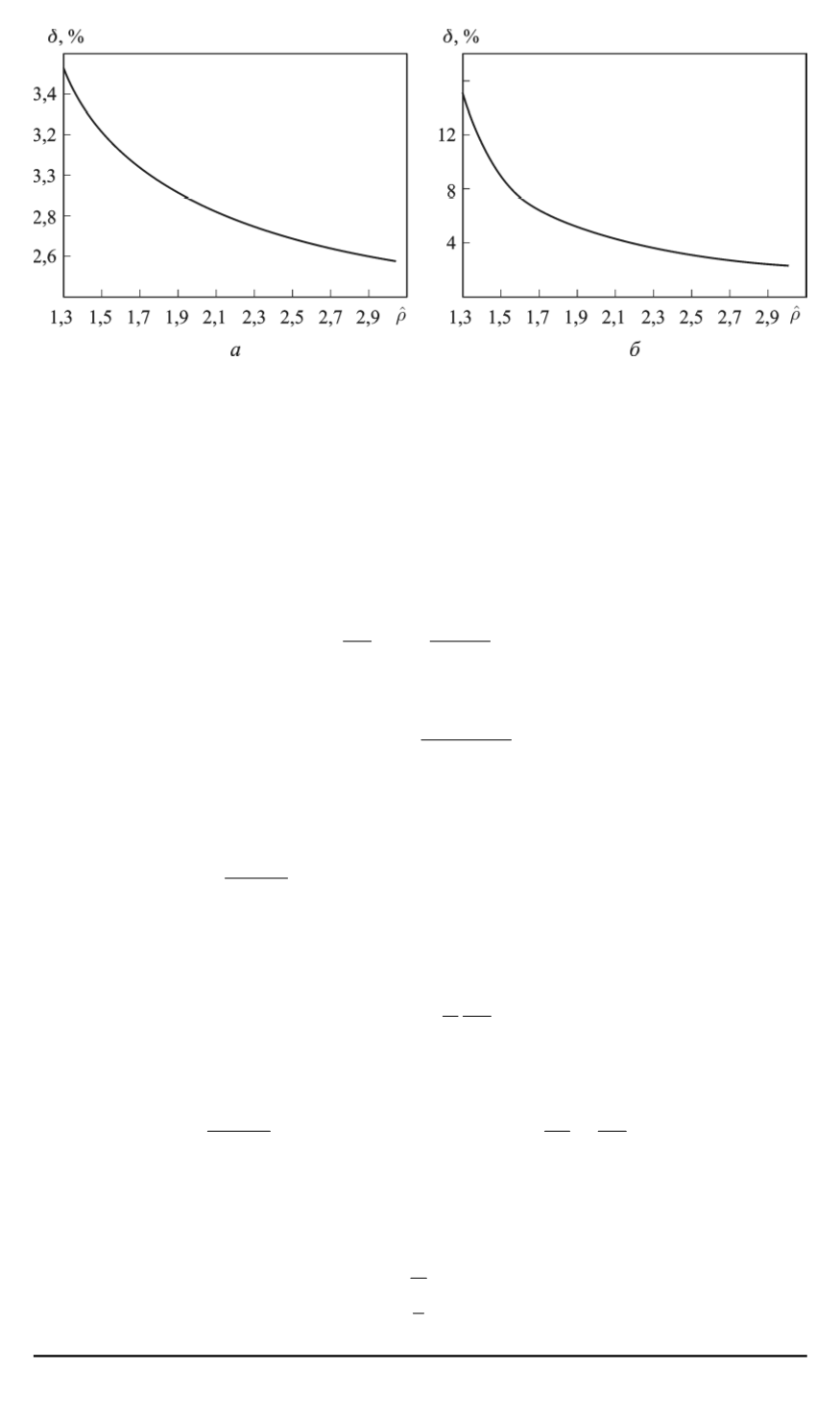
Рис. 3. Относительная погрешность определения времени достижения мак-
симума плотности нейтронов
t
m
по формуле (5) в сравнении с моделью
Нордгейма–Фукса (
а
) и
n
по модели Нордгейма–Фукса в сравнении с шести-
групповой моделью
приведенное в работе
1
, избыточно упрощено и не позволяет это реа-
лизовать.
Интегрируя уравнение, полученное из модели (2) путем исключе-
ния времени
t
,
dn
dρ
=
−
ρ
−
β
αK`
,
определяем
n
=
A
−
(
ρ
−
β
)
2
2
αK`
.
Вычислив постоянную интегрирования
А
из начальных условий
(
t
= 0;
ρ
=
ρ
0
;
n
=
n
0
)
, запишем выражение для
n
(
ρ
)
:
n
=
1
2
αK`
2
αK`n
0
+ (
ρ
0
−
β
)
2
−
(
ρ
−
β
)
2
.
Из первого уравнения модели Нордгейма–Фукса (2) выделим вы-
ражение для реактивности
ρ
=
β
+
`
n
dn
dt
и подставим его в выражение для плотности нейтронного потока:
n
=
1
2
αK`
"
2
αK`n
0
+ (
ρ
0
−
β
)
2
−
`
2
n
2
dn
dt
2
#
.
(6)
Обозначив
2
αK`
=
a
;
2
αK`n
0
+ (
ρ
0
−
β
)
2
=
b
;
`
2
=
c
;
r
b
c
=
γ,
(7)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2013. № 3 7


