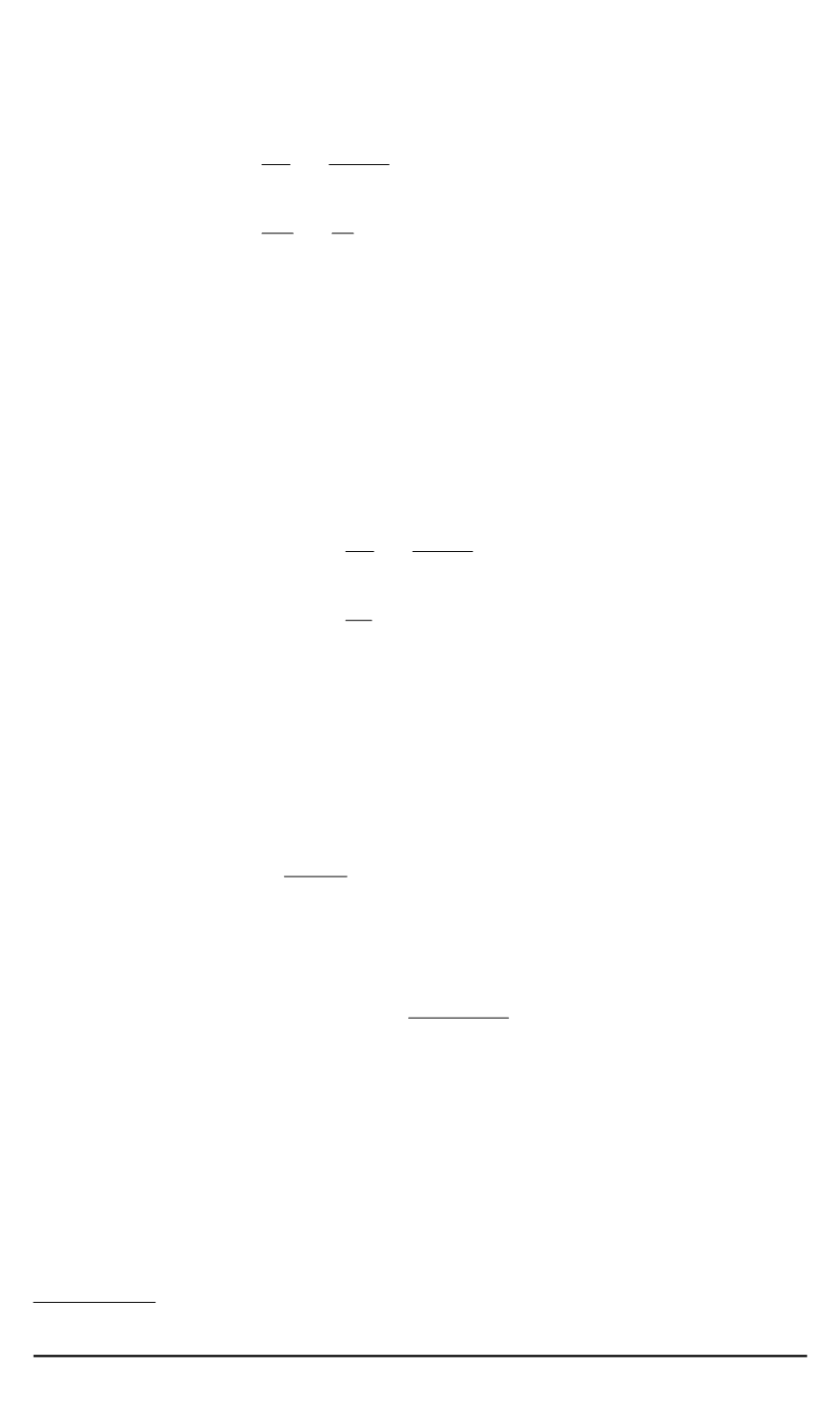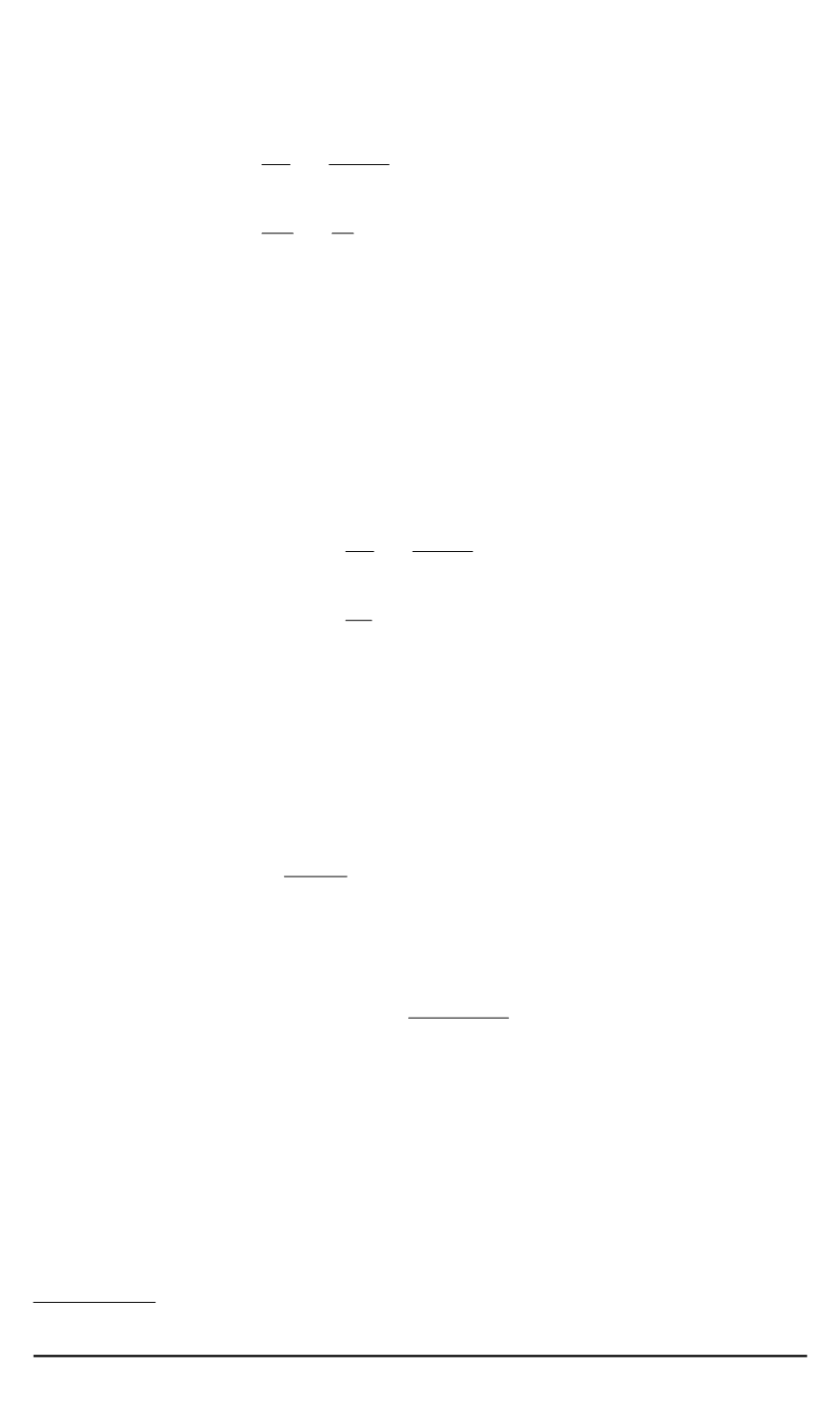
реактор в надкритическое состояние по мгновенным нейтронам
1
— это
так называемая адиабатическая модель, или модель Нордгейма–Фукса.
Модель выводится из общей системы уравнений
dn
dt
=
ρ
−
β
`
n
+
X
i
λ
i
c
i
+
q
;
dc
i
dt
=
β
i
`
n
−
λ
i
c
i
i
= 1
. . .
6
.
(1)
В модели принимается во внимание только генерация мгновенных
нейтронов, вклад других источников нейтронов (запаздывающих и ис-
точниковых) считается пренебрежимо малым. Другим, упрощающим,
положением модели Нордгейма–Фукса является адиабатичность про-
цесса, т.е. пренебрежение потерями теплоты, отводимыми от активной
зоны за время, описываемое моделью.
С указанными упрощениями система уравнений, описывающих по-
ведение реактора, согласно модели Нордгейма–Фукса имеет вид
dn
dt
=
ρ
−
β
`
n
;
dρ
dt
=
−
α
К
n.
(2)
При рассмотрении модели Нордгейма–Фукса для определения по-
стоянной интегрирования из начальных условий принимают, что плот-
ность нейтронов в начальный момент времени пренебрежимо мала
1
,
т.е.
n
0
= 0
, что не приводит к заметным погрешностям даже при воз-
мущениях, не слишком превышающих
β
. Тогда уравнение фазовой
траектории принимает вид
n
=
1
2
αK`
(
ρ
0
−
β
)
2
−
(
ρ
−
β
)
2
,
(3)
позволяющий, в частности, определить максимальное значение плот-
ности нейтронов в импульсе:
n
max
=
(
ρ
0
−
β
)
2
2
αK`
.
(4)
Эта формула дает результаты, мало отличающиеся от результатов
расчета по шестигрупповой модели кинетики (1) с учетом уравне-
ния, описывающего адиабатическую обратную связь (второе уравне-
ние системы (2)). Относительная погрешность расчета
n
max
снижается
с увеличением возмущения
ρ
0
(рис. 1), рассчитанного для
`
= 10
−
4
с и
αK
= 0
,
0025
. При этом числовые значения погрешности при варьиро-
вании указанных параметров даже на порядки значений изменяются
очень незначительно.
1
Хетрик
Д. Динамика ядерных реакторов. М.: Атомиздат, 1975. 400 с.
4 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2013. № 3