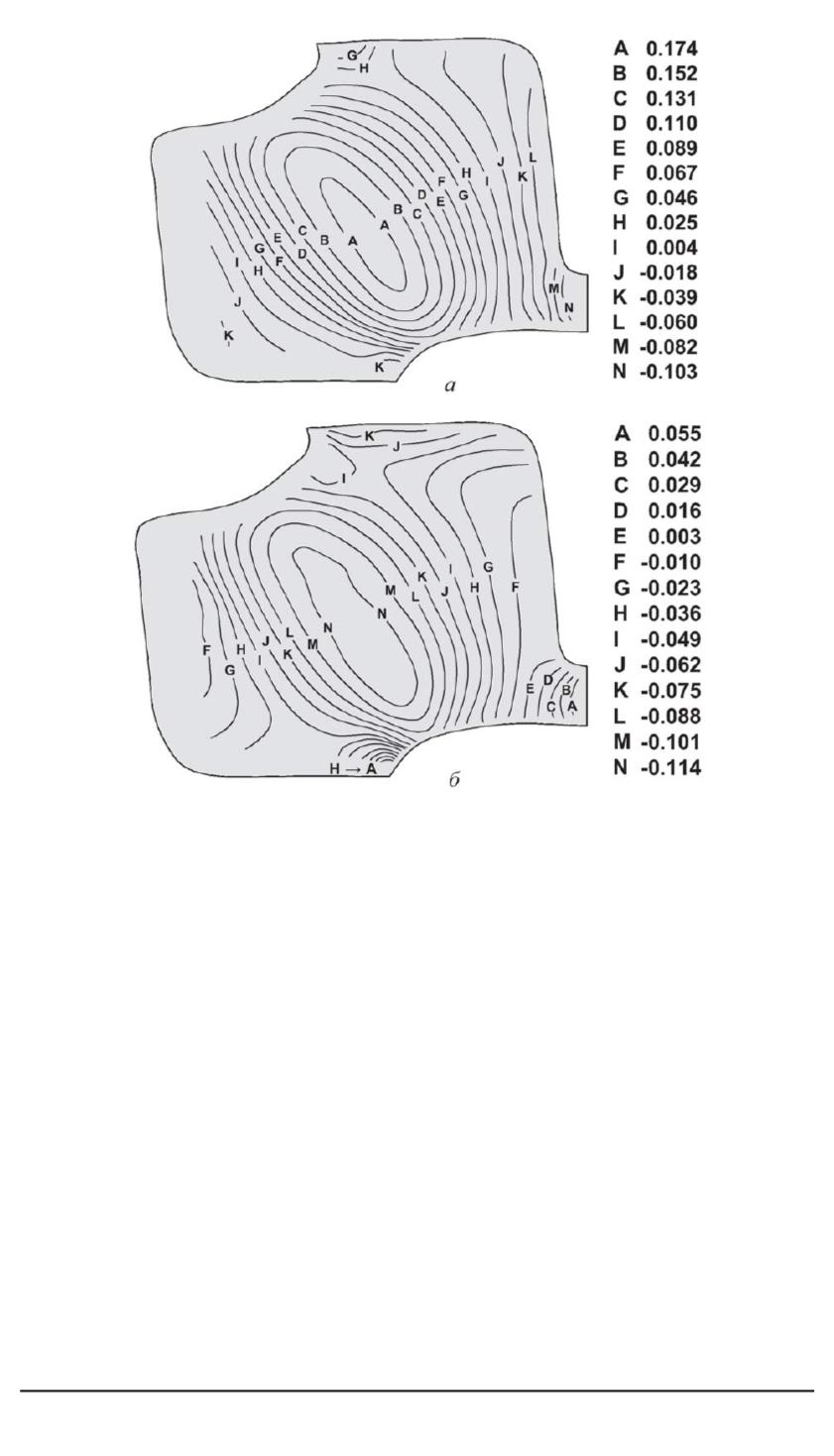
Рис. 8. Деформации
ε
11
(
а
) и
ε
22
(
б
) (эксперимент)
В целом полученные расчетные и экспериментальные данные, до-
полняя друг друга, даютпредставление о деформациях резиновой де-
тали амортизатора во всем ее объеме.
Вывод
. Выполненные расчеты свидетельствуют об удовлетвори-
тельных вычислительных свойствах четырехугольных четырехузло-
вых конечных элементов смешанного метода в задачах с возможным
объемным заклиниванием из-за малой сжимаемости материала. Раз-
работанная математическая модель обеспечивает весьма точное опре-
деление жесткости амортизатора.
СПИСОК ЛИТЕРАТУРЫ
1. Б е л к и н А. Е., С е м е н о в В. В., С е м е н о в В. К. Численный ана-
лиз больших плоских деформаций арочного амортизатора // Вестник МГТУ
им. Н.Э. Баумана. Сер. Машиностроение. – 2011. – № 2. – С. 55-64.
2. B a t h e K. J. Finite element procedures. – Prentice-Hall, Cliffs. – 1996. – 1036 p.
3. Д е м и д о в С. П. Теория упругости. – М.: Высш. шк., 1979. – 432 с.
10 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 2


