сываются следующим образом:
S
11
=
GJ
−
2
/
3
1
−
1
3
I
1
C
J
−
2
C
22
+
pJ
−
1
C
22
,
S
22
=
GJ
−
2
/
3
1
−
1
3
I
1
C
J
−
2
C
11
+
pJ
−
1
C
11
,
S
12
=
1
3
GJ
−
8
/
3
I
1
C
C
12
−
pJ
−
1
C
12
,
где
J
=
C
11
C
22
−
C
2
12
,
I
1
C
=
C
11
+
C
22
+ 1
.
Далее приведены результаты расчетного и экспериментально-
го определения деформаций амортизатора А-2000. В расчетах мо-
дули упругости резины имели следующие значения:
G
= 1
МПа,
k
= 2400
МПа. Отметим, что в теории малых деформаций отношению
модулей
k/G
= 2400
соответствует значение коэффициента Пуассона
0,4998, весьма близкое к значению 0,5 для абсолютно несжимаемого
материала.
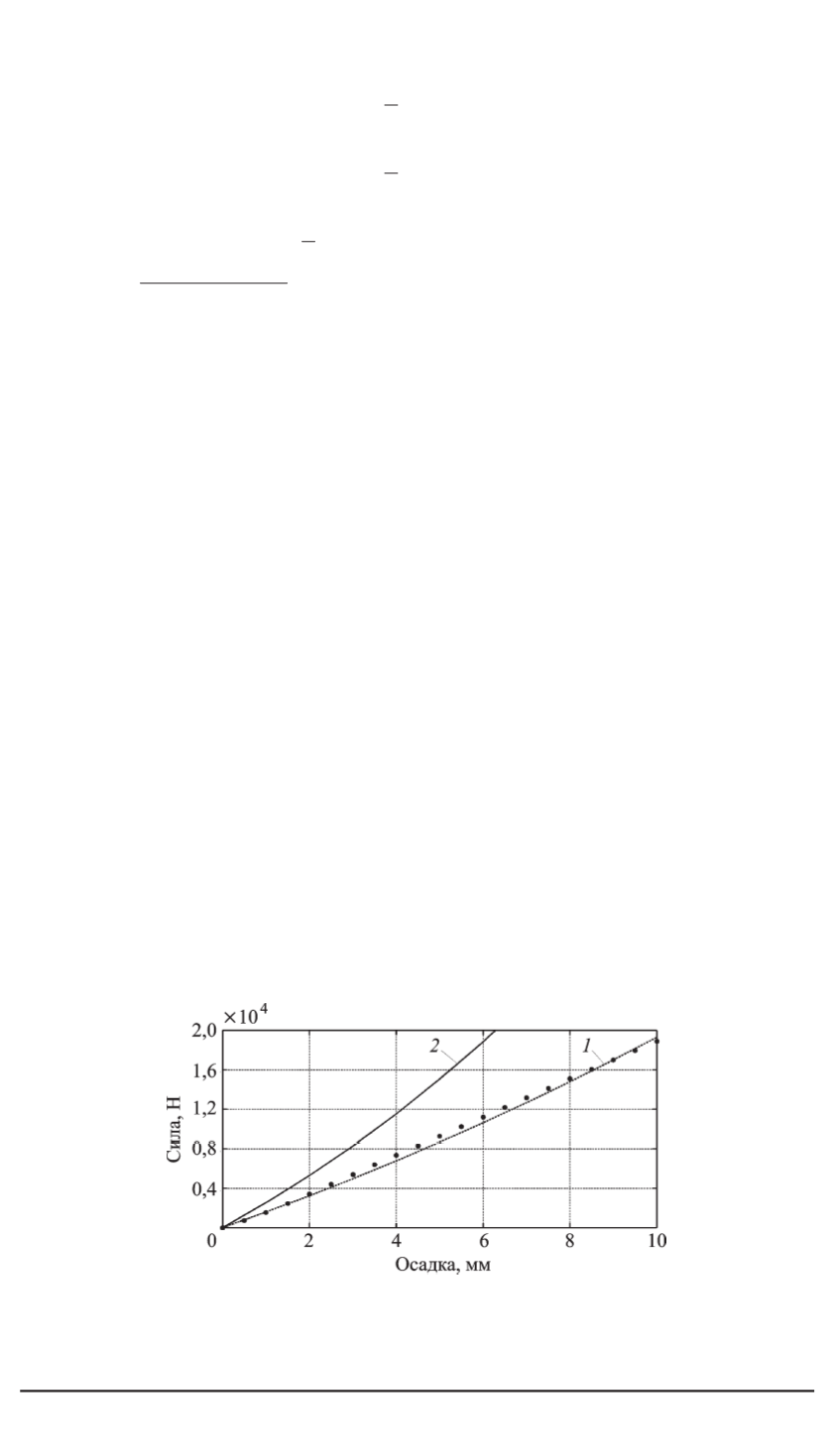
На рис. 5 показаны полученные нагрузочные характеристики амор-
тизатора, дающие представление о близости теоретических и экспери-
ментальных результатов. Видно, что смешанный метод обеспечивает
весьма точное определение жесткости резиновой детали. В расчетах
по методу перемещений жесткость существенно завышается из-за по-
грешностей в вычислениях объемной деформации и гидростатическо-
го давления.
На рис. 6 и 7 показаны изолинии полей деформаций в поперечном
сечении амортизатора при осадке 10 мм, полученные с использовани-
ем МКЭ. Приведенные результаты соответствуют состоянию резины
в области, удаленной от торцов амортизатора, т.е. в его центральной
части, где справедлива принятая в расчетах схема плоской деформа-
ции.
Вблизи торцов наблюдается существенная депланация поперечных
сечений, условие плоской деформации не выполняется. Деформации
Рис. 5. Нагрузочная характеристика амортизатора А-2000:
точки — результаты эксперимента; кривые
1, 2
— расчетные характеристики,
полученные смешанным методом и методом перемещений
8 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 2


