
=
Z
vol
[
B
]
t
[
D
]
{
e
th
}
d
(
vol
)
— вектор тепловых нагрузок для элемен-
та;
[
M
e
] =
ρ
Z
vol
{
N
}
T
{
N
}
d
(
vol
)
— матрица масс элемента;
{
u
00
}
=
=
∂
{
u
}
/∂t
2
— вектор ускорения (аналогичен силе тяжести);
{
F
e
}
pr
=
Z
areap
{
N
}
T
{
P
}
d
(
areap
)
— вектор сил давления.
В точках интегрирования элемента деформации вычисляются по
уравнению
{
ε
el
}
= [
B
]
{
u
} − {
ε
th
}
,
где [
B
] — матрица деформации-перемещения в точке интегрирования;
{
u
} — вектор узловых перемещений;
{
e
th
}
— вектор температурных
деформаций.
Три значения главных деформаций
ε
0
представляют собой корни
кубического уравнения, определяемого компонентами вектора дефор-
маций:
ε
X
−
ε
0
1
/
2
ε
XY
1
/
2
ε
XZ
1
/
2
ε
XY
ε
Y
−
ε
0
1
/
2
ε
Y Z
1
/
2
ε
XZ
1
/
2
ε
Y Z
ε
Z
−
ε
0
= 0
.
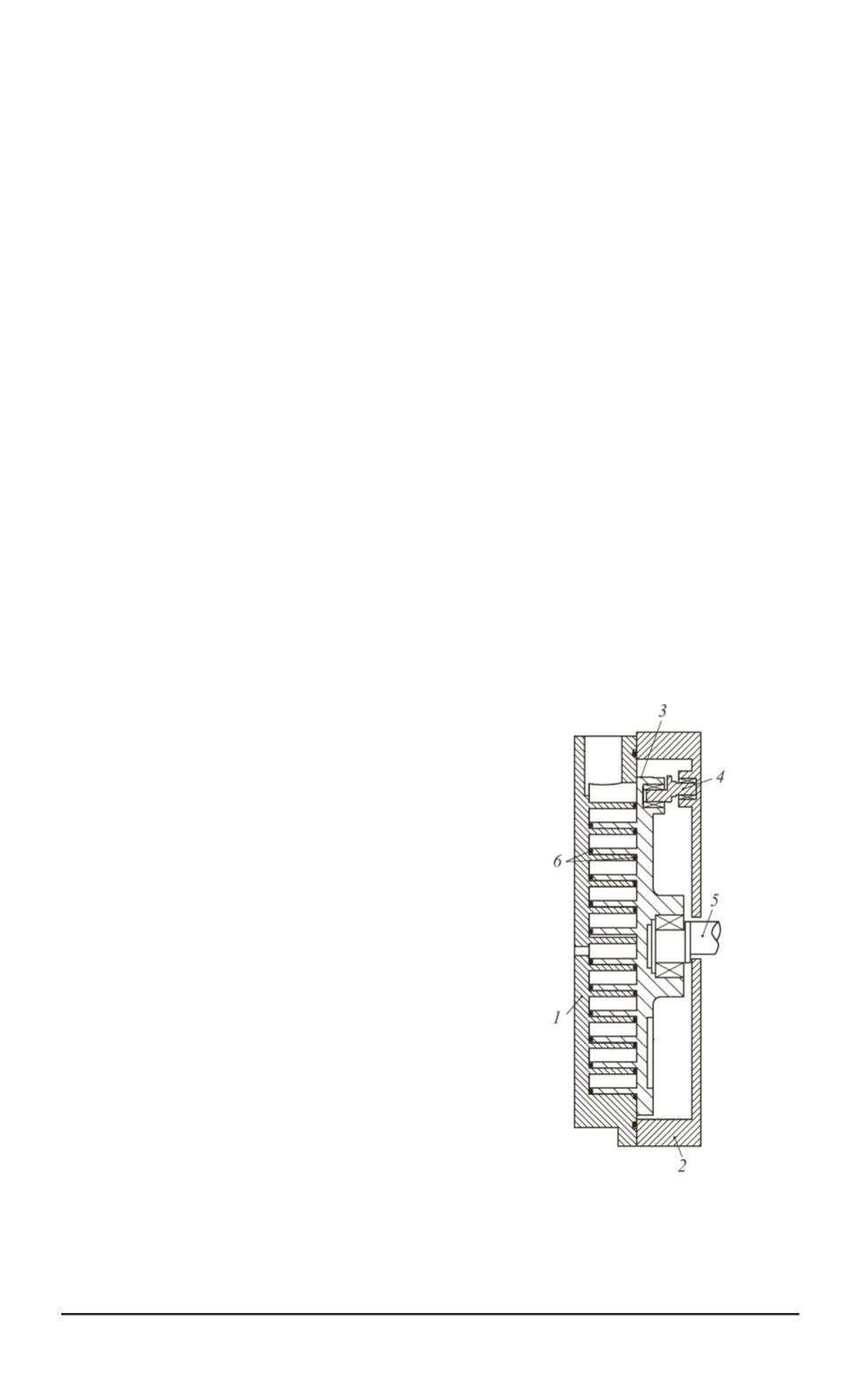
Рис. 6. Схема НВСп:
1, 2
— неподвижные элементы,
3
—
подвижный элемент,
4
— противо-
поворотные устройства,
5
— эксцен-
триковый приводной вал,
6
— торце-
вые уплотнители
Эквивалентные деформации е
вычисляются по формуле
ε
e
= (
S
[(
ε
1
−
ε
2
)
2
+(
ε
2
−
ε
3
)
2
+(
ε
3
−
ε
1
)
2
])
8
.
Расчетная схема НВСп приведена
на рис. 6.
Полученные компоненты векторов
деформаций с помощью команд пост-
процессора программного комплекса
ANSYS в трехмерной постановке вы-
водятся на экран в виде изолиний и
полей. Разработанная расчетная про-
грамма позволяет на основе исходных
данных получить деформированное
состояние подвижной и неподвижной
спиралей в осевом и радиальном на-
правлениях.
На рис. 7 представлены радиаль-
ные и осевые тепловые перемещения
подвижного и неподвижного спираль-
ных элементов, полученные в середи-
не высоты спирали.
98 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















