
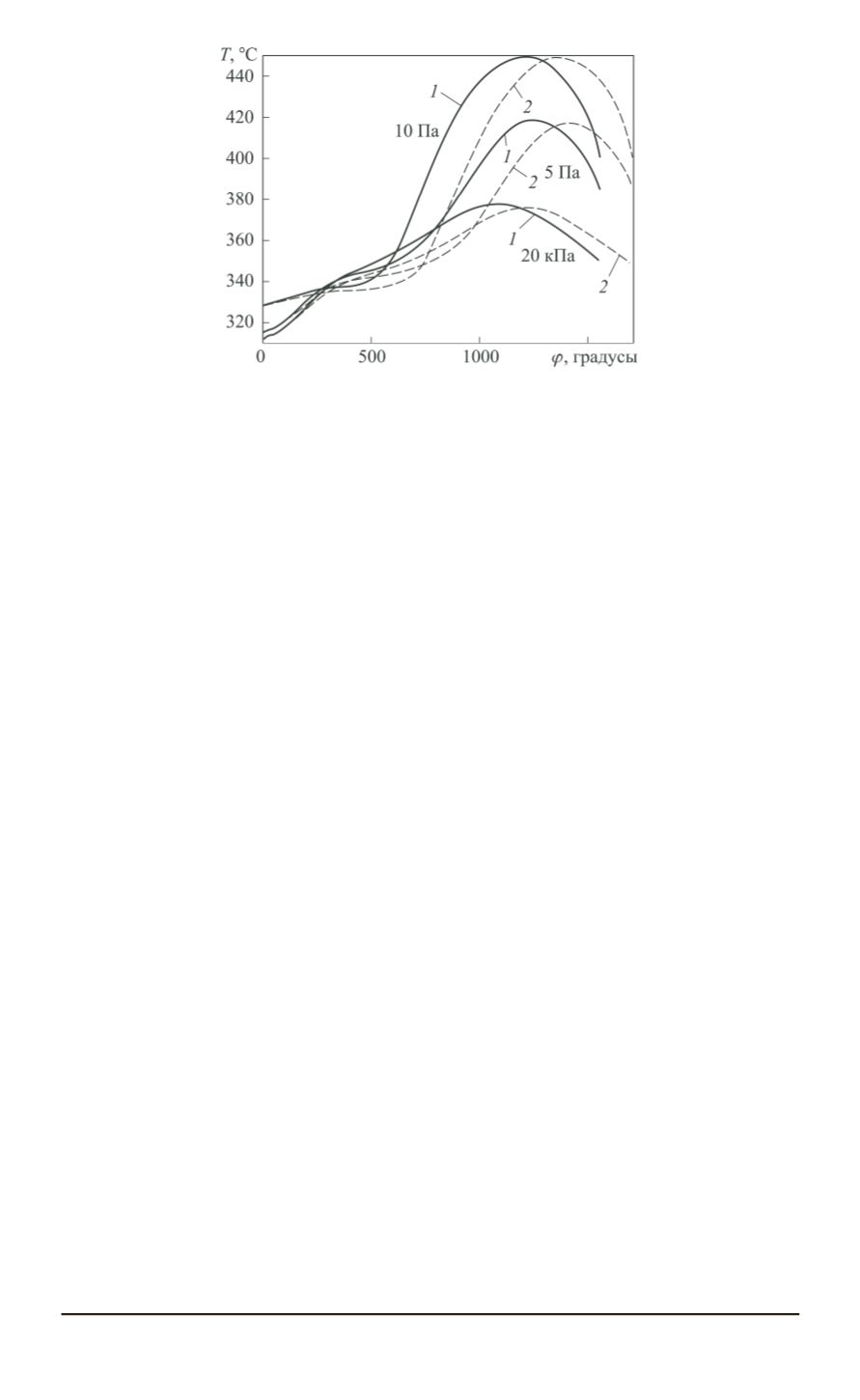
Рис. 3. Зависимость температуры газа от угла поворота подвижного спирально-
го элемента при различных входных давлениях; кривая
1
— полость
1
; кривая
2
— полость
2
ру газа около конечной площадки,
q
(
x
)
– дополнительный тепловой
поток, например от трения.
Для определения
α
(
x
)
и
T
0
(
x
)
необходимо знать параметры газа
около каждой площадки, такие как давление и температура. Данные
параметры находятся из математической модели, представленной в
работе [5] в виде распределения температуры и давления по длине пера
спирали. Зависимости температуры газа от угла поворота подвижного
спирального элемента приведены на рис. 3.
Перед передачей значений температуры в качестве граничных
условий проводится их осреднение по времени.
При задании граничных условий на торцевом диске спирали (меж-
ду витками пера спирали) параметры газа находились как средневзве-
шенное значение параметров ближайших двух точек, лежащих на раз-
ных витках.
После проведения расчета в термодинамическую модель снова пе-
редается распределение температуры пера спирали по длине пера для
уточнения расчета и организуется итерационный процесс расчета.
В результате расчета определяют температурные поля подвижного
и неподвижного спиральных элементов. В качестве примера на рис. 4
приведены распределения температур по поверхностям спиральных
элементов для входного давления
P
вх
= 5
кПа.
Для определения напряжений и деформаций в спиральных элемен-
тах НВСп использовался метод конечных элементов, который реали-
зован в программном комплексе “ANSYS” [5–7].
Подвижный и неподвижный спиральные элементы разбиваются на
тетраэдральные конечные элементы (рис. 5). Ансамбль из всех конеч-
ных элементов и узлов является основной конечно-элементной моде-
лью деформируемого тела.
96 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















