
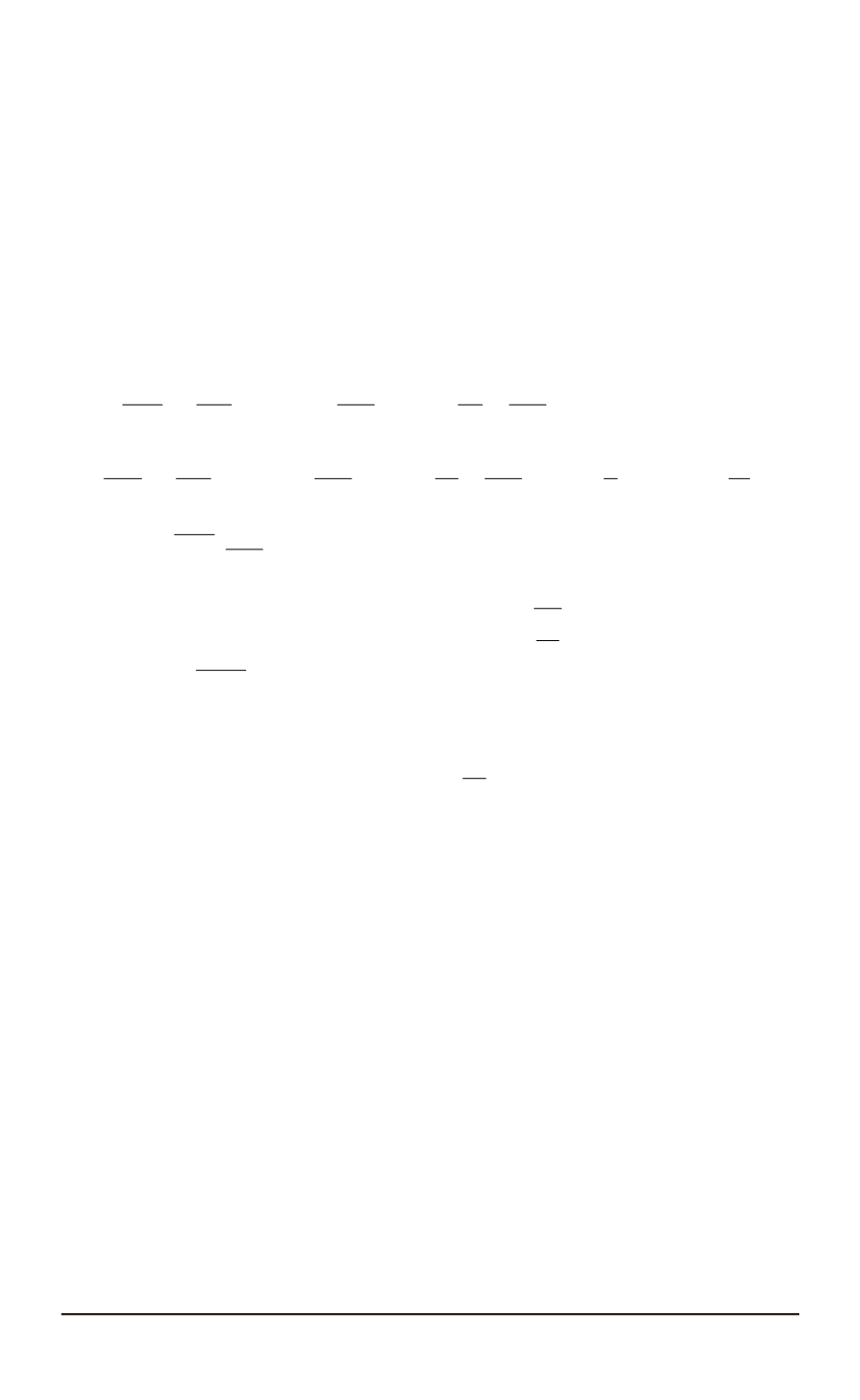
температурах, а для моделей без подводящего участка — в задании рав-
номерного распределения расхода воздушного потока по сечению ма-
кетов. На выходе из моделей задано равномерное распределение ста-
тического давления. Твердые поверхности расчетных моделей пред-
полагаются адиабатическими с выполнением условия прилипания.
Численное моделирование проводилось с помощью программно-
го комплекса ANSYS Fluent 15.0 [5] с использованием стандартной
(
k
–
ε
)-модели турбулентности [6].
Уравнения переноса без учета влияния плавучести и дополнитель-
ных источников генерации и порождения диссипации турбулентности
записываются в следующем виде:
∂ρk
∂t
+
∂
∂x
i
(
ρku
i
) =
∂
∂x
j
μ
+
μ
t
σ
k
∂k
∂x
j
+
G
k
−
ρε
−
Y
k
;
∂ρε
∂t
+
∂
∂x
i
(
ρεu
i
) =
∂
∂x
j
μ
+
μ
t
σ
ε
∂ε
∂x
j
+
C
1
ε
ε
k
G
k
−
C
2
ε
ρ
ε
2
k
,
где
G
k
=
ρu
0
i
u
0
j
∂u
j
∂x
i
— генерация турбулентной кинетической энергии;
Y
k
= 2
ρεM
2
t
— фактор, учитывающий условия сжимаемости течения
потока воздуха как идеального газа; M
t
=
r
k
a
2
— турбулентное число
Маха;
a
=
√
γRT
— скорость звука в потоке воздуха.
Турбулентная динамическая вязкость определяется по следующему
соотношению:
μ
t
=
ρC
μ
k
2
ε
.
Для данной модели использован стандартный набор констант:
С
1
ε
= 1
,
44
,
С
2
ε
= 1
,
92
,
С
μ
= 0
,
09
,
σk
= 1
,
0
,
σ
ε
= 1
,
3
.
Свойства воздуха описывались законом идеального газа.
Сходимость полученного численного решения проверялась по ра-
венству расходов на входе и выходе из пучка стержней. Из условия
сходимости вычислений для достижения погрешности определения
расходов не более 0,1% требовалось проведение не менее 2000 итера-
ций.
Полученные при численном моделировании результаты приведе-
ны для двух характерных областей течения: области регулярного рас-
положения стержней (центральный стержень) и причехловой области
(соседний к угловому стержень). Для каждого из стержней на радиусе,
соответствующем полувысоте дистанционирующего ребра, выбрано 5
точек диагностики, размещенных относительно друг друга с шагом
30
◦
.
Рассматриваемые характерные области течения и точки диагности-
ки показаны на рис. 1.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 7

















