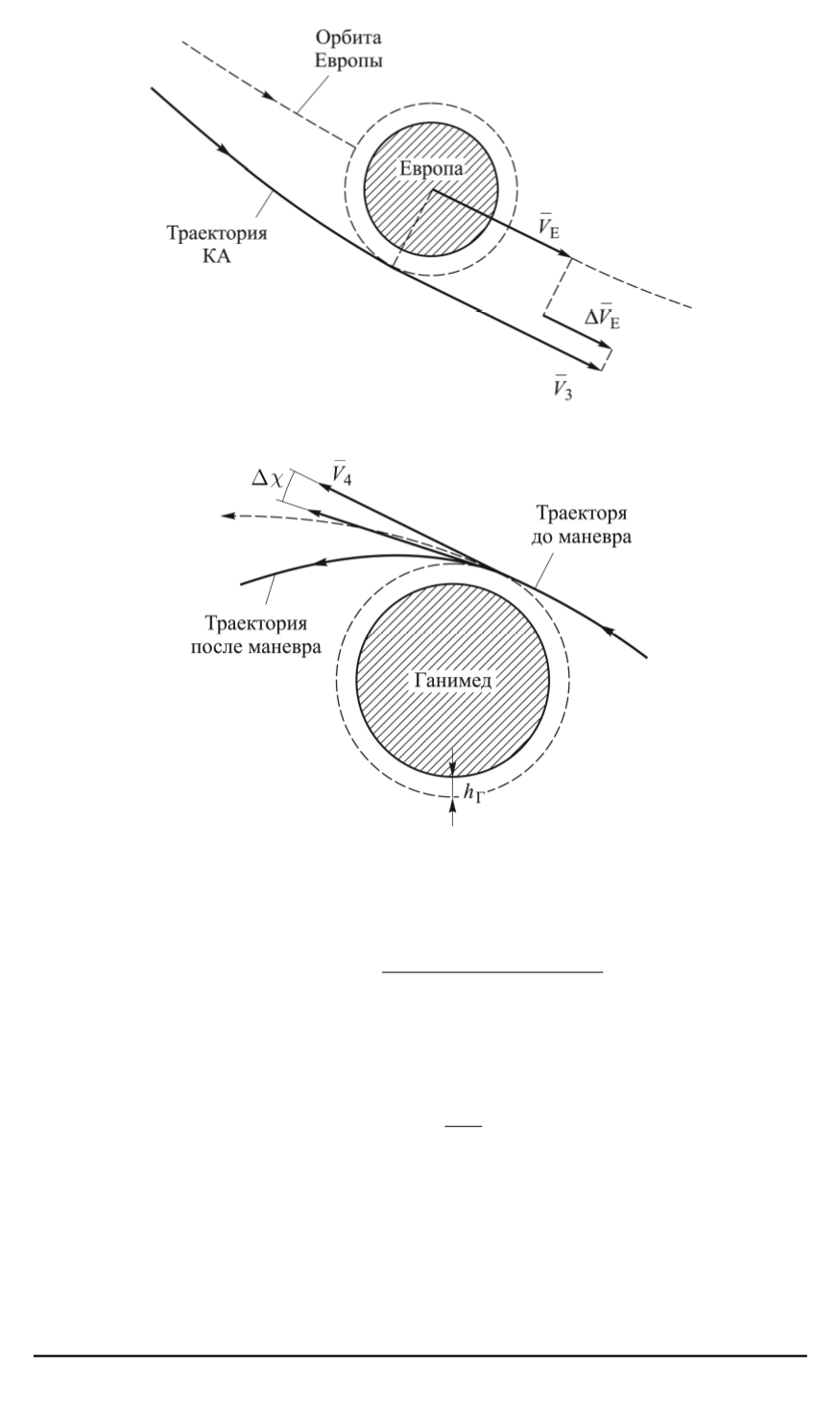
Рис. 4. Гиперболический избыток скорости КА после выполнения маневра
Рис. 5. Схема пролета Ганимеда
на который поворачивается вектор скорости за один пролет:
Δ
χ
= 2 arcsin
μ
Г
μ
Г
+ (
R
Г
+
h
Г
)Δ
V
2
4
,
где
μ
Г
— гравитационный параметр Ганимеда;
R
Г
— радиус Ганимеда;
h
Г
— высота пролета КА над поверхностью Ганимеда.
Тогда число пролетов Ганимеда, необходимых для поворота векто-
ра скорости на угол
χ
, составит
n
=
χ
Δ
χ
.
Пример расчета.
Определим затраты импульса на формирова-
ние орбиты ИСЕ для двух случаев: в первом случае КА выходит на
орбиту Европы без совершения каких-либо маневров, во втором пред-
варительно выполняет некоторое число пролетов в сфере действия
Ганимеда. Значения физических параметров тел Солнечной системы,
используемые в расчете, указаны в [4, 5].
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 4 57


