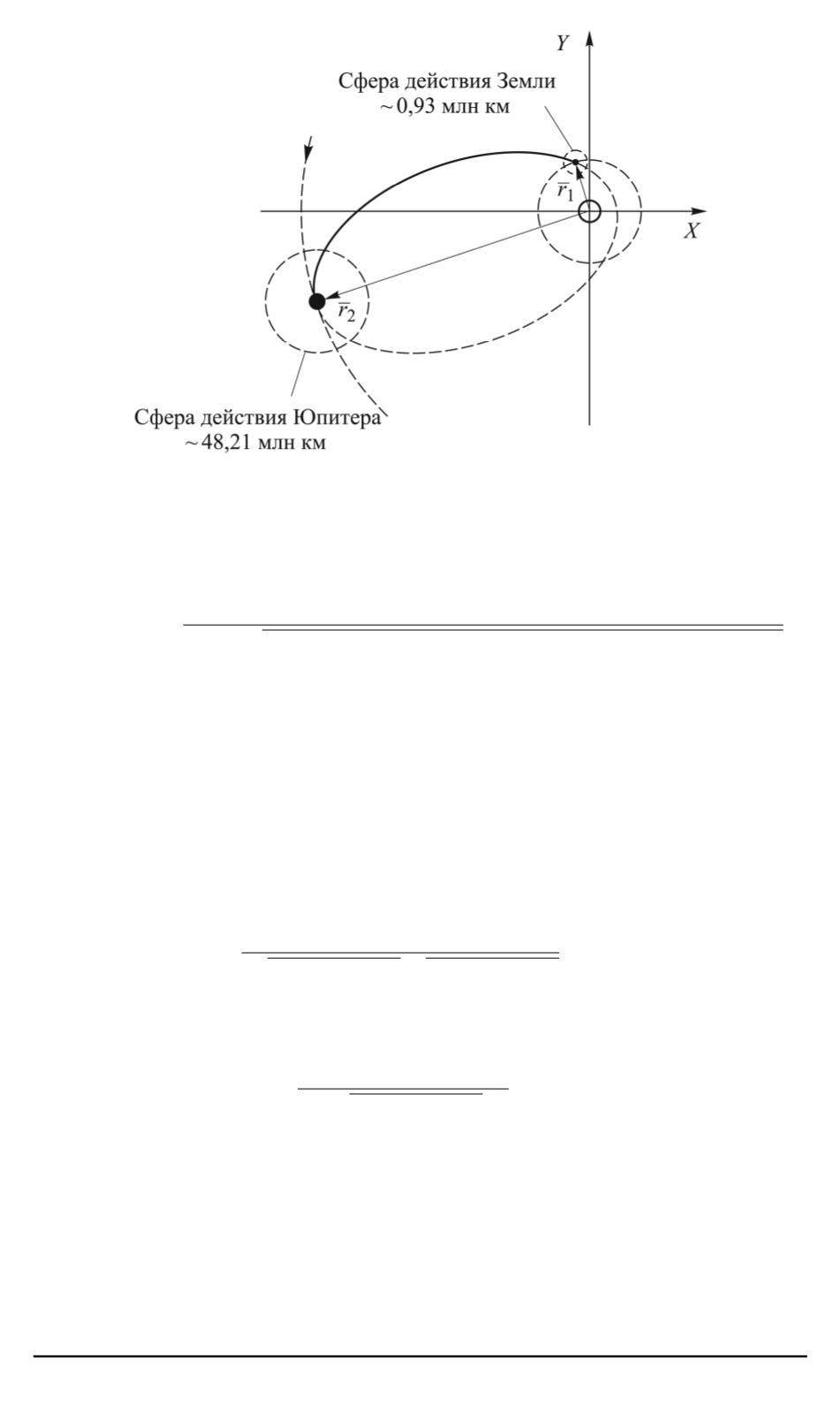
Рис. 1. Траектория перелета Земля –Юпитер
Долгота восходящего узла:
Ω
г
= arcsin
(
y
1
z
2
−
y
2
z
1
) sign (
x
1
y
2
−
x
2
y
1
)
sin
i
г
q
(
y
1
z
2
−
y
2
z
1
)
2
+ (
x
2
z
1
−
x
1
z
2
)
2
+ (
x
1
y
2
−
x
2
y
1
)
2
,
Ω
г
2
[0
,
2
π
]
.
Долгота восходящего угла
Ω
г
и наклонение
i
г
гелиоцентрического
участка траектории КА полностью определяют положение плоскости
перелета в эклиптической системе координат.
Угловая дальность гелиоцентрического участка:
Δ
ϑ
= arccos
"
x
1
x
2
+
y
1
y
2
+
z
1
z
2
p
x
2
1
+
y
2
1
+
z
2
1
p
x
2
2
+
y
2
2
+
z
2
2
#
,
Δ
ϑ
2
(0
,
2
π
)
.
Аргумент широты:
u
i
= arccos
"
x
i
cos Ω
3
+
y
i
sin Ω
3
p
x
2
i
+
y
2
i
+
z
2
i
#
, u
i
2
[0
,
2
π
]
.
Вычисление элементов орбиты в плоскости перелета сводится к
решению задачи Ламберта. С помощью соотношений, приведенных
в работе [2], определим большую полуось
a
г
, эксцентриситет
e
г
, ар-
гумент перицентра
ω
г
, время пролета перицентра
t
п
и угол
ϑ
i
(угол
между направлением восходящего узла гелиоцентрической траектории
и радиус-вектором положения планеты).
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 4 53


