Рис. 2. Гиперболический избыток ско-
рости КА относительно Европы
где
Δ
V
i
=
q
Δ
V
2
xi
+ Δ
V
2
yi
+ Δ
V
2
zi
,
μ
п
i
— гравитационный параметр
планеты.
Истинная аномалия бесконеч-
но удаленной точки и аргумент
перицентра:
θ
г
i
= arccos
−
1
e
г
i
;
ω
3
i
=
u
3
i
−
θ
3
i
.
Более подробно с используе-
мыми в расчетах соотношениями
можно ознакомиться в [2].
Гравитационные маневры в
сфере действия Ганимеда.
В ре-
зультате расчета межпланетной траектории получаем необходимый
стартовый импульс аппарата
Δ
V
1
и гиперболический избыток
Δ
V
2
скорости КА относительно Юпитера.
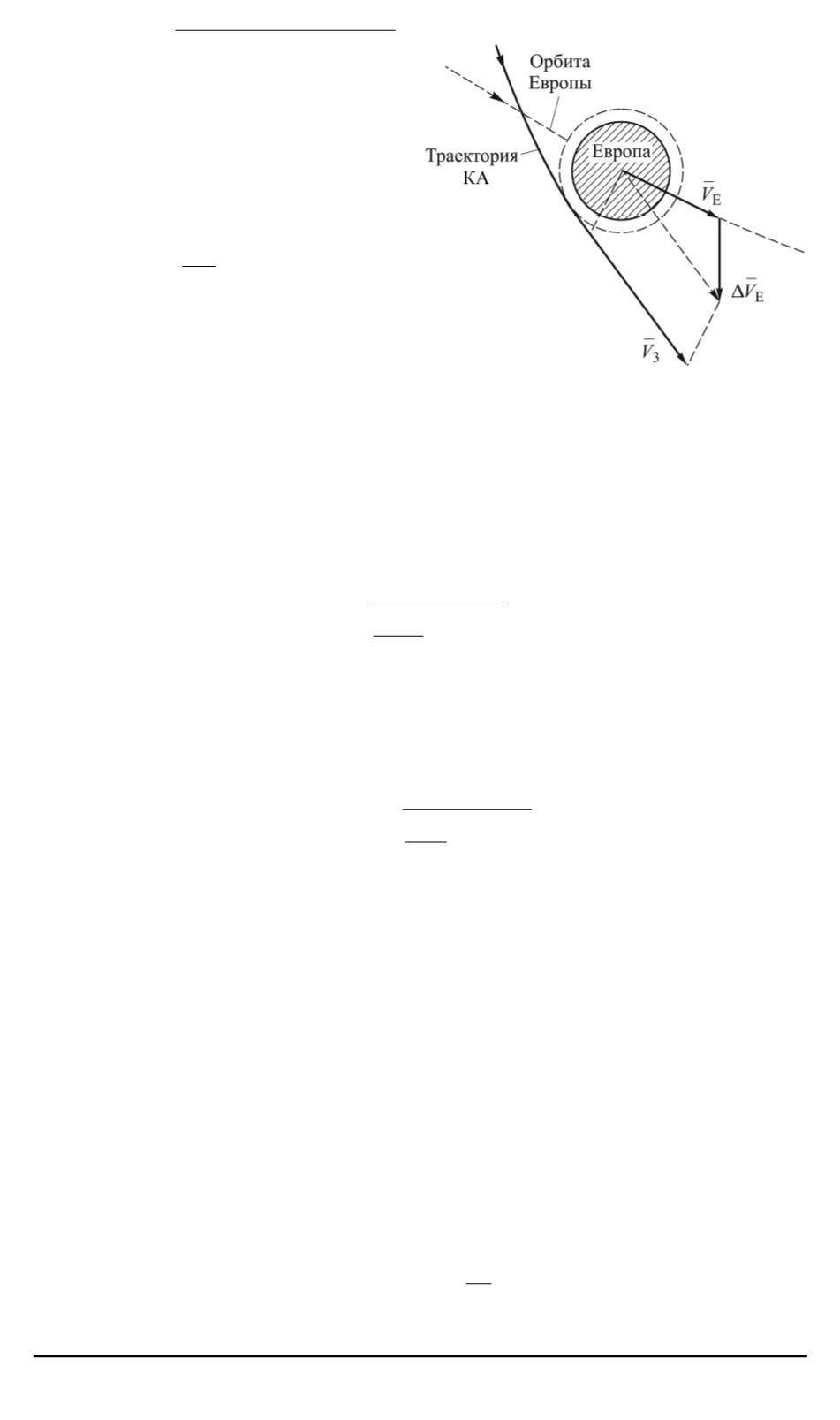
Гиперболический избыток скорости относительно Европы (рис. 2)
составит
Δ
V
3
=
r
2
μ
Ю
r
Е
+ Δ
V
2
2
−
V
Е
,
где
μ
Ю
— гравитационный параметр Юпитера;
r
Е
— средний радиус
орбиты Европы;
V
E
— средняя орбитальная скорость Европы.
Тормозной импульс для выхода на круговую экваториальную ор-
биту Европы (без выполнения промежуточных маневров) равен
Δ
V
=
r
2
μ
E
r
o
+ Δ
V
2
3
,
(1)
где
μ
E
— гравитационный параметр Европы;
r
o
— радиус орбиты ИСЕ.
Рассмотрим возможность снижения значения тормозного импульса
с помощью гравитационных маневров в сфере действия Ганимеда.
Порядок проведения маневра состоит в следующем: пролет Юпитера
и выход на экваториальную орбиту его искусственного спутника с
апоцентром в районе орбиты Ганимеда, поворот вектора скорости КА
за счет его гравитационного поля и выход на орбиту Европы. Схема
маневра изображена на рис. 3 (промежуточные орбиты не показаны).
Пусть
V
π
— скорость КА сразу после пролета Юпитера и радиус
перицентра орбиты
r
π
=
R
Ю
+
h
Ю
, где
R
Ю
— радиус Юпитера, а
h
Ю
— высота пролета КА над планетой. Используя интегралы энергии,
площадей и геометрические соотношения, получаем:
Δ
V
2
3
= 3
V
2
Е
−
V
2
Г
+ Δ
V
2
4
−
2
r
Г
r
Е
V
Е
−
V
Г
Δ
V
4
cos
ψ,
(2)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 4 55


