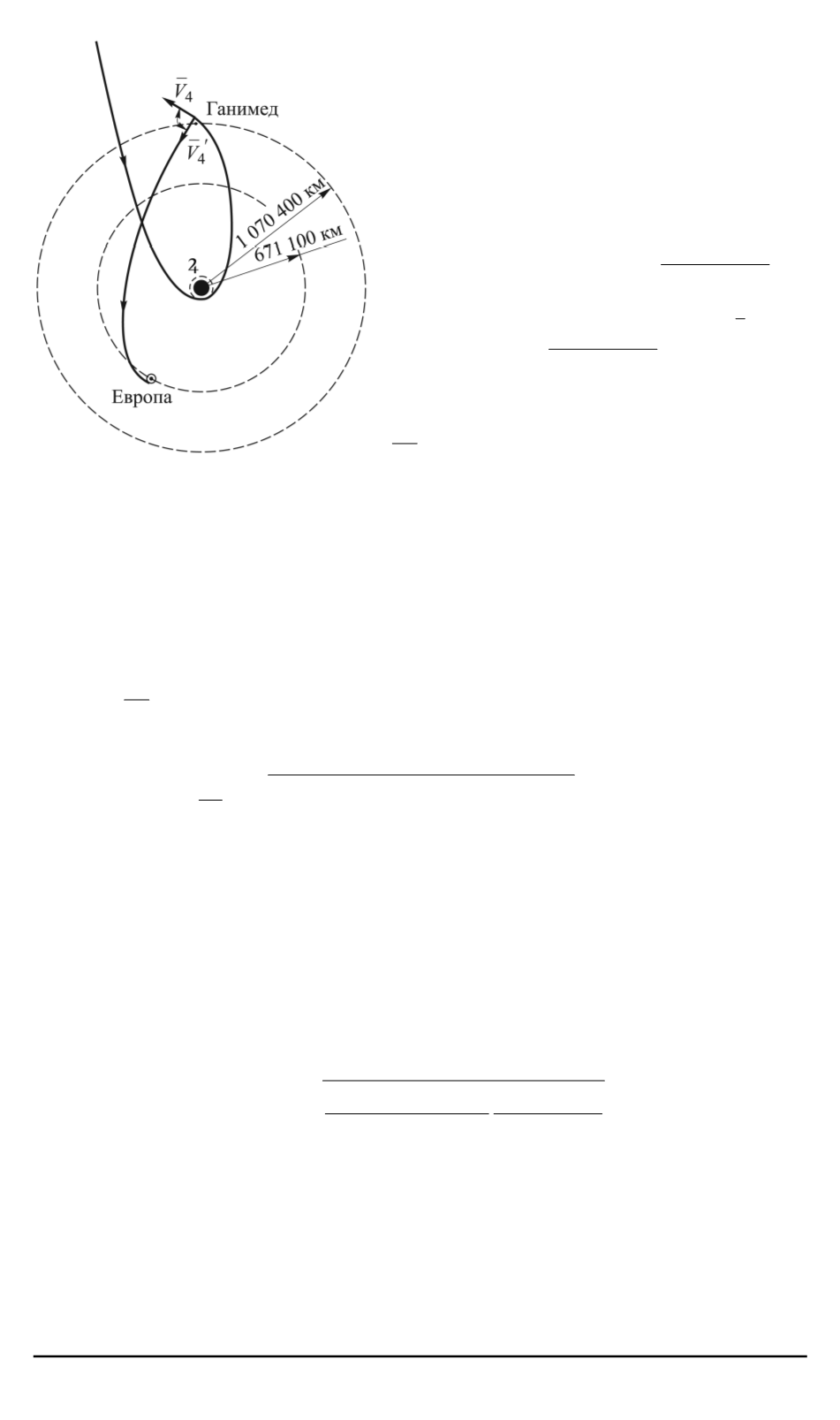
Рис. 3. Общая схема маневра
где
V
Г
— средняя орбитальная ско-
рость Ганимеда;
r
Г
— средний ради-
ус орбиты Европы;
ψ
— угол между
векторами
−→
V
Г
и
−−→
Δ
V
4
;
Δ
V
4
— гипербо-
лический избыток скорости КА отно-
сительно Ганимеда:
Δ
V
4
= 3
V
2
Г
+
V
2
π
−
2
μ
Ю
R
Ю
+
h
Ю
−
−
2
R
Ю
+
h
Ю
r
2
V
Г
V
π
1
2
.
(3)
Из (2) следует, что поскольку
r
Г
r
Е
V
Е
> V
Г
, то минимальное значе-
ние
Δ
V
3
достигается при максималь-
ном значении
cos
ψ
. Это выполняется
при
ϕ
1
=
\
−→
V
Е
,
−→
V
3
= 0
, где
−→
V
3
— скорость КА вблизи Европы.
Используя интегралы площадей и геометрические соотношения,
получаем:
V
3
=
ρ
(
V
Г
+ Δ
V
4
cos (
ψ
))
,
(4)
где
ρ
=
r
Г
r
Е
.
Подставляя
V
3
из (3) в геометрические соотношения, найдем
Δ
V
4
cos
ψ
=
1
ρ
2
q
(2
ρ
3
−
3
ρ
2
+ 1)
V
2
Г
+
ρ
2
Δ
V
2
4
−
ρ
2
−
1
V
Г
.
(5)
Подставляя (5) в (2), с учетом (3) получаем, что минимальное зна-
чение
Δ
V
3
достигается при минимальном значении
V
π
. Последнее
условие выполняется, если у начальной траектории КА радиус апо-
центра
r
α
=
r
2
, т.е.
ϕ
0
2
=
ψ
0
= 0
, где
ϕ
0
2
=
\
(
−→
V
Г
,
−→
V
0
4
)
,
ψ
0
=
\
(
−→
V
Г
,
−−→
Δ
V
0
4
)
,
−→
V
0
4
— скорость КА после облета Ганимеда,
Δ
−→
V
0
4
— гиперболический
избыток скорости КА после облета Ганимеда.
В этом случае скорость КА в апоцентре орбиты
V
α
=
r
2
μ
Ю
R
Ю
+
h
Ю
+
r
Г
R
Ю
+
h
Ю
r
Г
и
Δ
V
4
=
V
Г
−
V
α
.
Из (4) и (5) определим
V
3
. Поскольку
ϕ
1
= 0
, то
Δ
V
3
=
V
3
−
V
Е
(рис. 4). Тогда из (1) находим тормозной импульс для выхода на орбиту
Европы.
Из (5) определим угол
χ
, на который должен быть повернут вектор
скорости КА в результате облетов Ганимеда (рис. 5). Определим угол,
56 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 4


