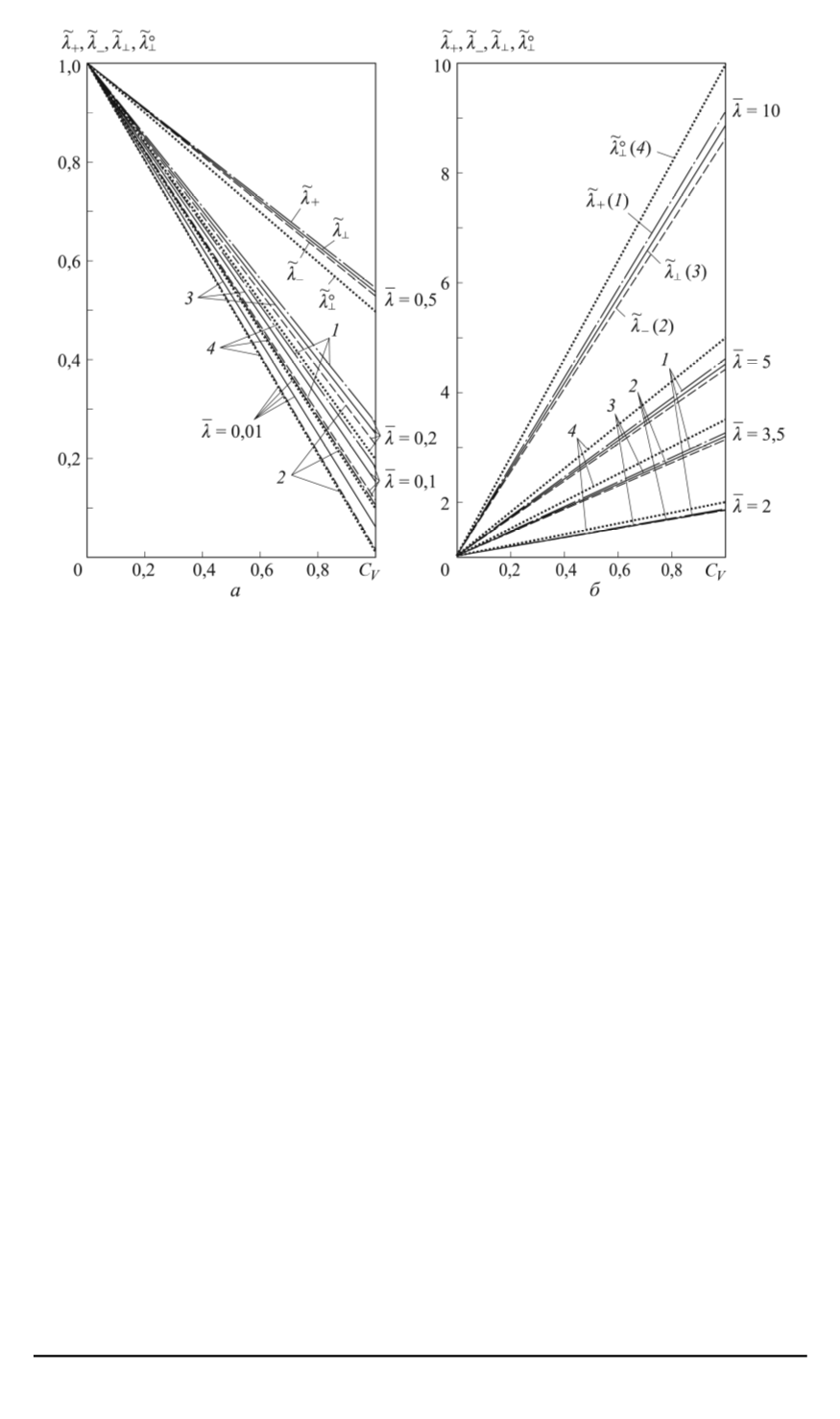
Рис. 2. Графики зависимостей при
ˉ
λ <
1 ˉ
λ
верхней
˜
λ
+
˜
λ
(штрихпунктирные
линии) и нижней
˜
λ
−
˜
λ
(штриховые линии) оценок эффективного коэффициента
теплопроводности
˜
λ
?
˜
λ
(сплошные кривые) от объемной концентрации
C
V
волокон и аналогичных зависимостей
˜
λ
◦
?
˜
?
λ
(пунктирные линии) от
C
V
при
r
0
/r
1
= 0
,
9
,
ˉ
λ
= (1 + ˉ
λ
)
/
2
ˉ = ( ˉ
λ
λ
и различных значениях
ˉ
λ <
1 ˉ
λ
(
а
) и
ˉ
λ >
1 ˉ
λ
(
б
)
при
C
V
>
0
по формуле (12) для значений
ˉ
λ <
1
приводит к неравен-
ству
e
λ
◦
?
<
e
λ
?
, а для значений
ˉ
λ >
1
— к неравенству
e
λ
◦
?
>
e
λ
?
.
Сравнение на рис. 2 графиков зависимостей
e
λ
?
и
e
λ
◦
?
показывает,
что при значении
λ
?
= (
λ
◦
?
+
λ
m
)
/
2
, расположенном между значени-
ями коэффициентов теплопроводности для волокна и матрицы, вли-
яние промежуточного слоя на эффективный коэффициент теплопро-
водности композита достаточно мало. Для современных композитов
с полимерной матрицей и высокомодульными волокнами [1] харак-
терно неравенство
ˉ
λ >
1
. Например, для композита с арамидными
волокнами (кевлар-49) и эпоксидной матрицей
ˉ
λ
≈
30
[ 2 ]. Это об-
стоятельство при
λ
?
< λ
m
приводит к более существенному влиянию
промежуточного слоя на значение
λ
?
для композита в целом. На рис. 3
с использованием прежних обозначений приведены результаты расче-
тов при
r
0
/r
1
= 0
,
9
,
λ
?
=
λ
m
/
2
и различных значениях
ˉ
λ >
1
. Видно,
что различие между результатами расчетов по формулам (11) и (12)
растет по мере возрастания
C
V
и
ˉ
λ
. По-прежнему, каждая сплошная
кривая для зависимости
e
λ
?
от
C
V
при фиксированном значении пара-
метра
ˉ
λ
лежит в полосе между соответствующими штрихпунктирной и
64 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 1


