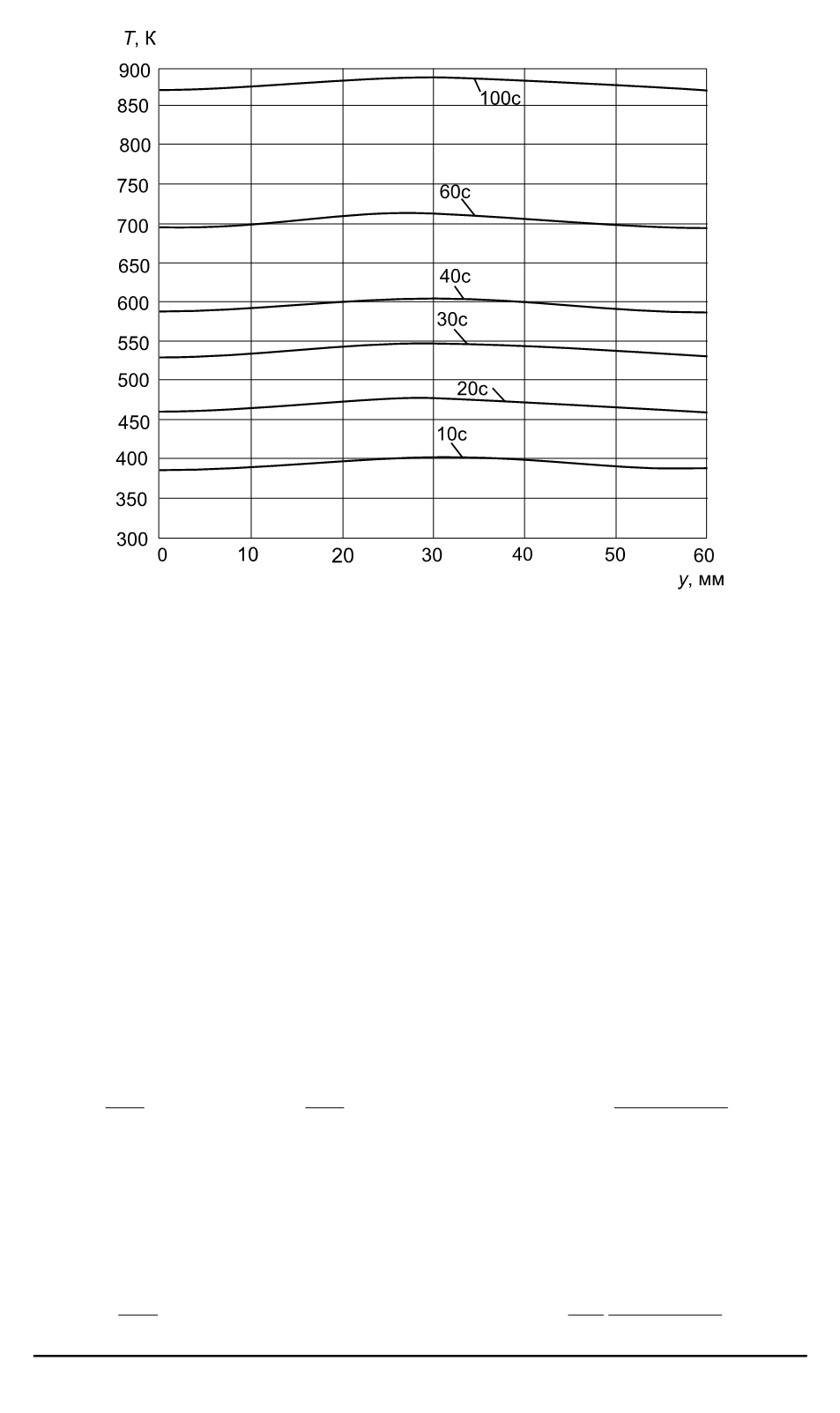
Рис. 3. Изменение температуры по фронтальной поверхности двухслойной пла-
стины при переменном тепловом потоке
В качестве примера на рис. 3 показано распределение темпера-
туры по фронтальной поверхности теплоизолированной с трех сто-
рон двухслойной пластины, состоящей из слоя молибдена толщи-
ной 2 мм и слоя керамики толщиной 30 мм, в различные моменты
времени, полученное с использованием МКЭ для случая синусои-
дального изменения падающего на поверхность потока излучения
q
пад
(
y
) =
q
пад,max
sin(41
y
+ 0
,
34)
.
При использовании МЭБ применялась явная конечно-разностная
схема [15], а исследуемая прямоугольная область разбивалась по тол-
щине на 65 слоев.
Для внутренних слоев материалов “2” и “1” (слои
i
= 1
, . . . ,
59
и
i
= 61
, . . . ,
63
) уравнение баланса тепловых потоков принимает вид
λ
(
j
)
Δ
x
(
T
k
i
−
1
−
T
k
i
) +
λ
(
j
)
Δ
x
(
T
k
i
+1
−
T
k
i
) =
c
(
j
)
ρ
(
j
)
Δ
x
T
k
+1
i
−
T
k
i
Δ
τ
,
где
Δ
τ
=
τ
k
+1
−
τ
k
— шаг интегрирования по времени; индекс
j
= 1
относится к молибдену;
j
= 2
— к подложке.
При записи уравнений баланса для граничных слоев учитывается
теплообмен с окружающей средой:
λ
(2)
Δ
x
(
T
k
1
−
T
k
0
) +
α
1
(
T
(1)
k
∞
−
T
k
0
) =
c
(2)
ρ
(2)
Δ
x
2
T
k
+1
0
−
T
k
0
Δ
τ
30 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 3


