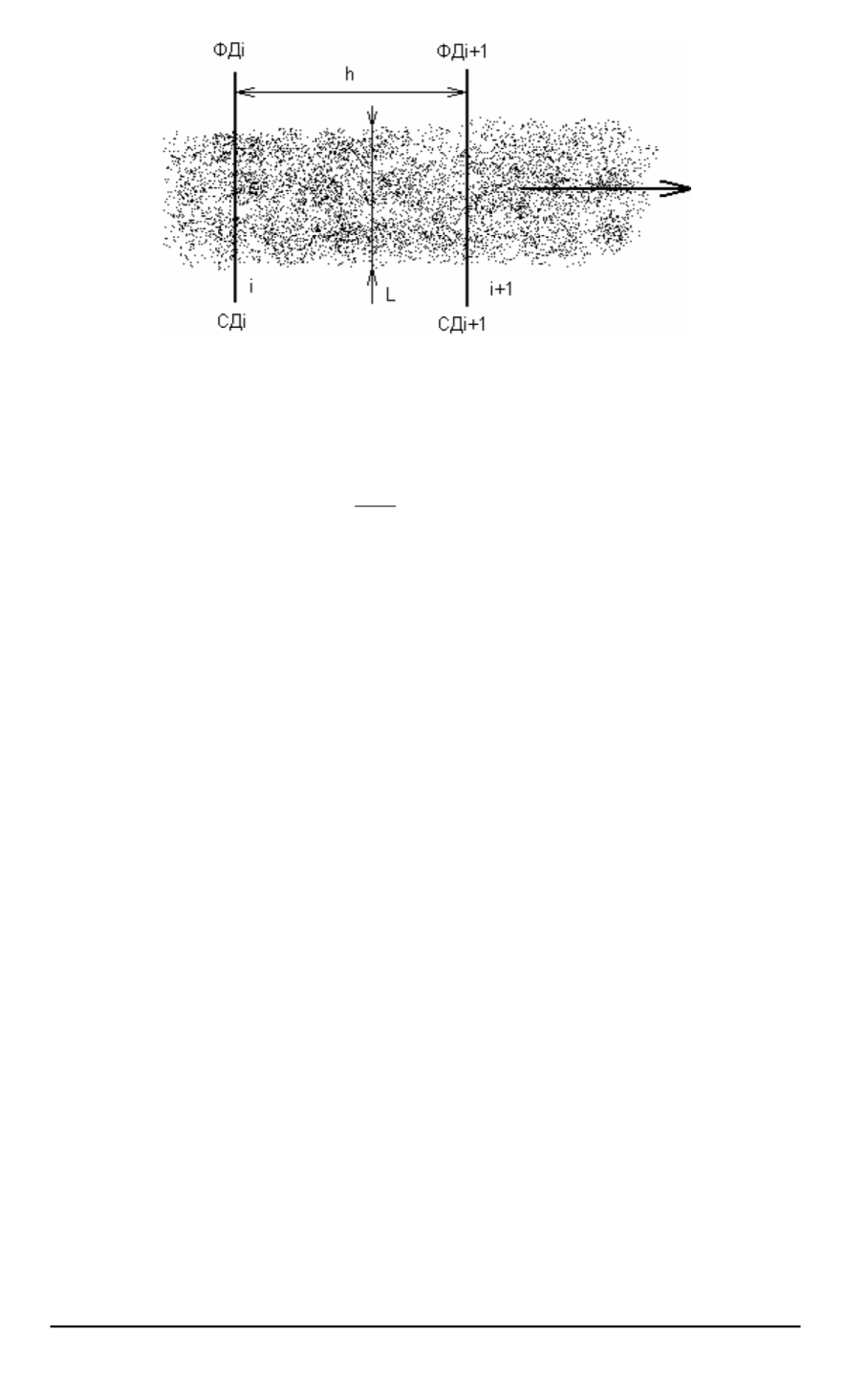
Рис. 1. Схема метода определения скоростных характеристик потока
По закону Бугера–Ламберта–Бера относительную интенсивность
светового излучения, прошедшего через среду, можно представить как
J
(
t
) =
I
(
t
)
I
0
= exp
{−
αnL
}
,
(1)
где
I
(
t
)
— интенсивность светового излучения, прошедшего через
импульсный дисперсный поток в произвольный момент времени
впрыска;
I
0
— интенсивность светового излучения в отсутствие дис-
персного потока;
α
— оптический коэффициент импульсного дис-
персного потока;
n
— концентрация частиц в объеме импульсного
дисперсного потока, пронизанного световым излучением;
L
— толщи-
на импульсного дисперсного потока в соответствующем сечении.
От значения параметра оптической толщины среды
τ
=
αnL
в
формуле (1) зависит вид рассеяния световой волны. Если
τ <
0
,
1
, то
рассеяние считается однократным, если
0
,
1
< τ <
0
,
3
, тогда необхо-
димо учитывать второе приближение многократного рассеяния, а если
τ >
0
,
3
, тогда имеет место многократное рассеяние. В разреженных
облаках, когда плотность капель мала, используют приближение од-
нократного рассеяния. Полагаем, что очень небольшое число капель
находится на пути световой волны и рассеянная волна определяется
однократным рассеянием на каплях. При увеличении плотности ка-
пель необходимо учитывать затухание вдоль пути распространения
волны из-за поглощения и рассеяния. Здесь используют первое при-
ближение многократного рассеяния. При распространении световых
монохроматических волн в случайных средах с невысокой плотно-
стью капель используют либо приближение однократного рассеяния,
либо теорию многократного рассеяния в первом приближении. С уве-
личением плотности среды случайных рассеивателей возрастает роль
некогерентной интенсивности рассеяного излучения по сравнению с
когерентной при малой плотности капель, и начинают сказываться эф-
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1 101


