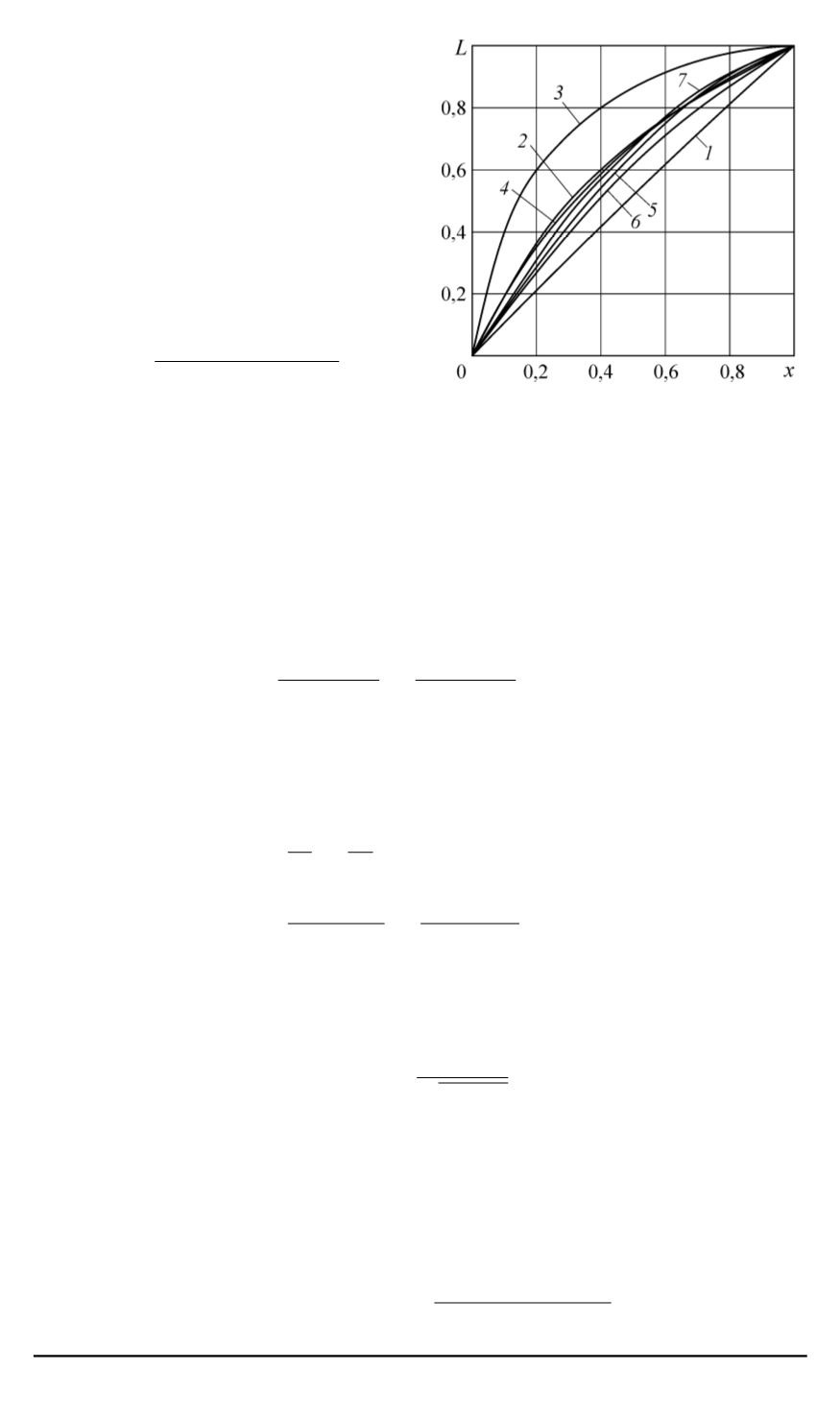
Рис. 2. Форма контура поковки:
1, 2
— кривые при
y
с
= 10
и 2 (урав-
нение (1));
3, 4
— окружности, проходя-
щие через крайние точки и пересекаю-
щие кривую, заданную уравнением (1);
5, 6
— гиперболы с коэффициентами
a
= 2
;
10
и
b
= 1; 3
соответственно;
7
— парабола
2. Окружность проходит че-
рез крайние точки с координата-
ми
(0
,
0)
,
(1
,
1)
и точку с коор-
динатами
(0
,
5
,
0
,
68)
, лежащую на
рассматриваемой кривой (
y
c
= 2
).
Понятно, что в этом случае дуга
окружности задана однозначно, а
ее центр лежит в некоторой произ-
вольной точке. При этом функция
(1) выглядит так:
L
(
х
) =
p
3
,
88
−
(1
,
8
−
x
)
2
−
0
,
8
.
Как видно из графика этой
функции, она почти полностью со-
впадает с исследуемой.
Гипербола.
Крайние точки с
координатами
(0
,
0)
и
(1
,
1)
соеди-
ним гиперболой. В каноническом
виде уравнение гиперболы
(
L
−
y
0
)
2
a
2
−
(
x
−
x
0
)
2
b
2
= 1
(2)
содержит четыре неизвестных:
a
,
b
,
x
0
,
y
0
. Выразим
x
0
,
y
0
через
a
и
b
.
Подставляя граничные условия
L
= 0
при
x
= 0
,
L
= 1
при
x
= 1
в
уравнение (2), получаем
y
2
0
a
2
−
x
2
0
b
2
= 1;
(1
−
y
0
)
2
a
2
−
(1
−
x
0
)
2
b
2
= 1
.
(3)
Используя вполне очевидные физические и геометрические огра-
ничения и считая
a
и
b
положительными числами, приходим к следу-
ющему неравенству:
a > b >
a
√
2
a
+ 1
.
Чтобы построить график гиперболы, зададим конкретные значения
параметров
a
и
b
, соблюдая полученное неравенство.
1. Пусть
a
= 2
,
b
= 1
. Тогда в соответствии с уравнениями (3)
имеем
x
0
= 1
,
129
,
y
0
= 3
,
016
.
Подставляя эти значения в уравнение (2), получаем
L
(
х
) = 3
,
016
−
2
p
1 + (
x
−
1
,
129)
2
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 4 61


