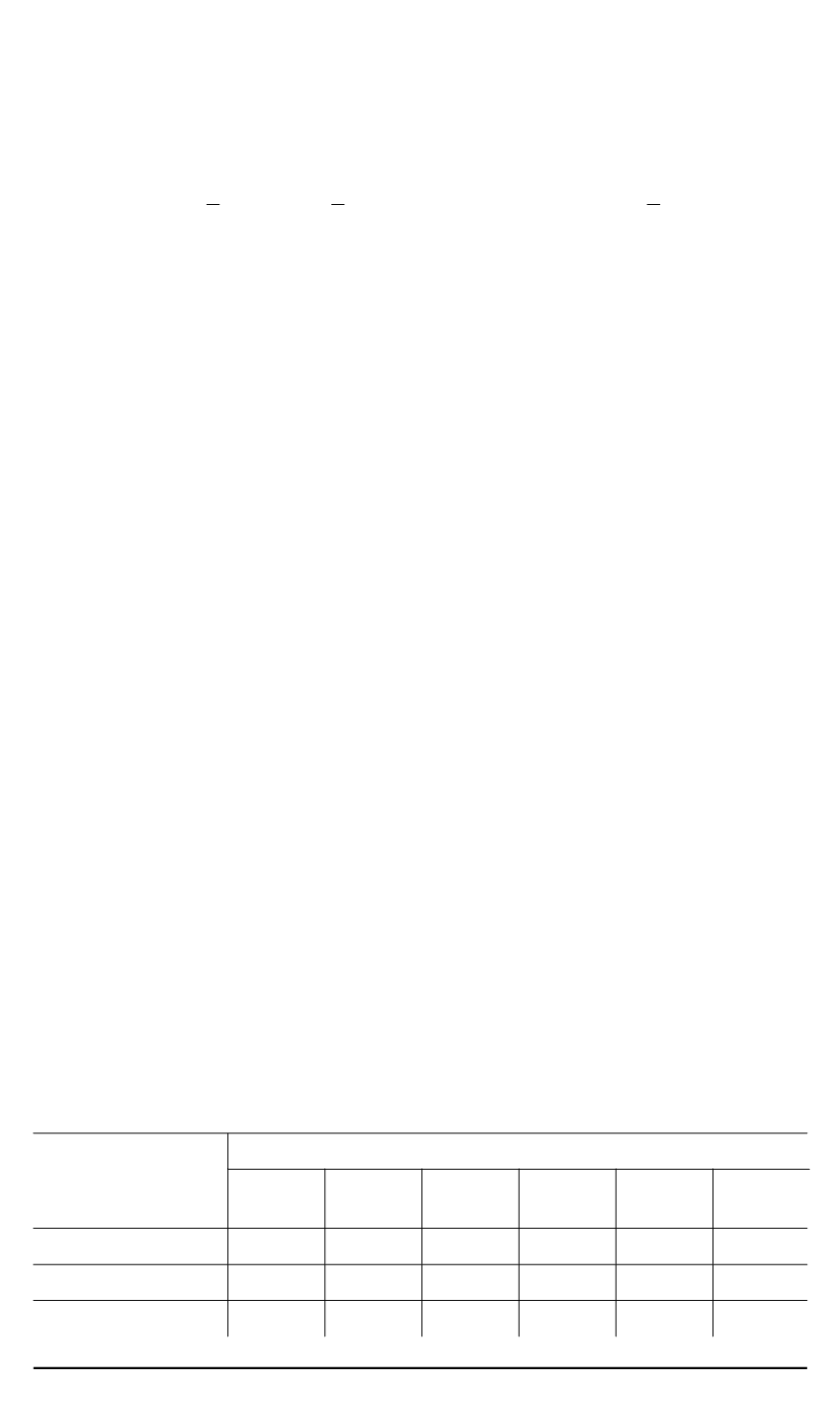
ν
31
=
ν
32
= (0
,
5
−
C
2
f
)
/
(1 +
C
3
f
) = (0
,
5
−
f
)(1
−
2
f
) = 0
,
5
(20)
— при сжатии;
ν
12
= (0
,
5 +
√
3
f
)
/
(1 +
√
3
f
)
>
0
,
5;
ν
31
= 0
,
5
/
(1
− √
3
f
)
>
0
,
5
(21)
— при чистом сдвиге, где принято
f
= Φ
d
/
3Φ
m
,
μ
≈
1
/
Φ
m
и
æ = 0
.
Из соотношений (19)–(21) следует, что на характеристики
E
i
и
ν
ij
влияют тригонометрические функции
C
i
, отражающие вид напря-
женного состояния. Результаты вычислений по соотношениям (19) и
(20) расходятся с результатами испытаний, представленными на рис. 4
начальными точками графиков
3
и
4
, тогда как расхождения с резуль-
татами вычислений по выражению (21) более приемлемы.
Если принять во внимание тот факт, что при деформировании сдви-
гом существенную роль играют главные касательные напряжения, то
допустимо состояние чистого сдвига дополнять для каждого исходно-
го с помощью величин
C
i
. Не нарушая соосности тензоров
σ
ij
и
ε
ij
и
вводя в рассмотрение функцию
q
= 1
/
(1 +
β
exp(
−
αξ
))
,
(22)
где
α
и
β
— коэффициенты, а
ξ
=
σ
0
/S
0
, можно внести изменения в
соотношения (19) и (20) с помощью следующего уравнения:
C
i
=
C
i
(1
−
q
) +
C
τi
q,
(23)
где
C
τi
— состояние чистого сдвига.
Выполненное наложение следует рассматривать как дополнение к
алгоритму, учитывающее наличие рассмотренного механизма дефор-
мации и позволяющее согласовать теорию с опытом. Результаты расче-
та начальных значений
ν
ij
с учетом уравнения (23) в виде табл. 1 дают
представление о их различии. Cреднее значение
ν
с
= 0
,
5
при всех
напряженных состояниях. Коэффициенты
α
и
β
подбирали, исходя из
условия лучшего согласования с опытными данными для начальных
значений
ν
при растяжении и сжатии.
Таблица 1
Коэффициенты поперечной деформации
Вид напряжен-
ного состояния
ν
12
ν
21
ν
13
ν
31
ν
23
ν
32
Растяжение
0,517 0,554 0,481 0,536 0,445 0,463
Чистый сдвиг
0,520 0,542 0,479 0,522 0,457 0,478
Сжатие
0,532 0,537 0,467 0,504 0,463 0,495
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3 11


