Выше отмечалось, что снижение плотности внутренних связей
учитывается переменной величиной
æ
. Как показано в работе [10],
она может быть принята в следующем виде:
æ = æ
u
S
m
u
,
(24)
где
S
u
=
S
0
/S
b
;
S
b
и
m
— постоянные величины. Интенсивность это-
го процесса существенно зависит от вида напряженного состояния и
гидростатического напряжения. Поэтому
æ
u
принята в виде функции,
аналогичной (22):
æ
u
= æ
0
/
[1 +
β
1
exp(
−
α
1
ξ
)]
,
(25)
где
æ
0
,
β
1
,
α
1
— постоянные величины. Их значения определяются
из условия лучшей аппроксимации экспериментальных графиков
ν
–
ε
.
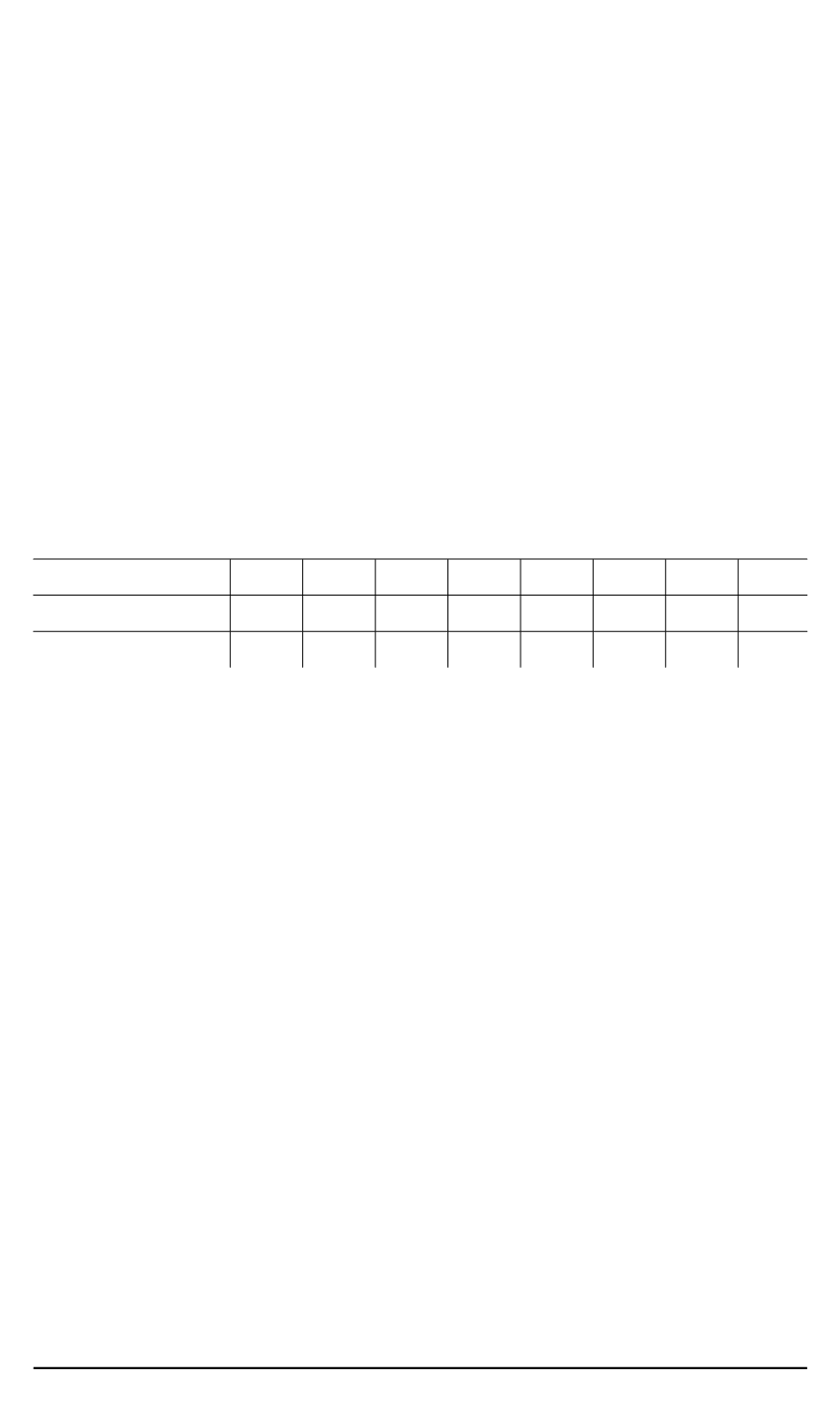
На рис. 4 эти графики представлены кривыми
5
и
6
, построенными по
данным из табл. 2.
Таблица 2
ε
∙
10
2
1,5 2,5 3,5 4,0 4,5 5,0 5,5 6,0
Растяжение (
ν
12
) 0,511 0,505 0,496 0,490 0,484 0,478 0,472 0464
Сжатие (
ν
31
) 0,503 0,504 0,505 0,506 0,507 0,508 0,510 0,512
Необходимо принять во внимание, что учет рассмотренных эф-
фектов по разработанной модели может внести поправки в расчет
напряженно-деформированного состояния изделий из ВНП только при
их малой деформации. Традиционные подходы, описывающие эту сре-
ду тензорно-линейными уравнениями, вполне оправданы.
Трудности с определением модулей упругости, как показано в ра-
боте [1], вполне преодолимы, если использовать не эксперименталь-
ные данные с прямым измерением поперечной деформации, а инте-
гральные результаты, которые следуют из испытаний с определением
объемной деформации. Однако при этом останутся скрытыми отме-
ченные эффекты и связанные с ними особенности упругих свойств.
Опытные и расчетные данные о начальных значениях
E
и
ν
, показы-
вают, что разномодульность ВНП реальна и ее следует учитывать при
анализе упругих свойств.
В заключение следует отметить, что рассматриваемые особенности
упругого поведения ВНП могут быть отражены в феноменологической
модели, включающей в себя тензорно-нелинейные уравнения связи де-
формаций с напряжениями и дополнения (23) и (24). Необходимость
подобных дополнений при описании поведения сложных сред под-
тверждают многие исследователи. Например, в работе [13] для учета
внутренних сдвиговых процессов главные компоненты обобщенного
12 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3


