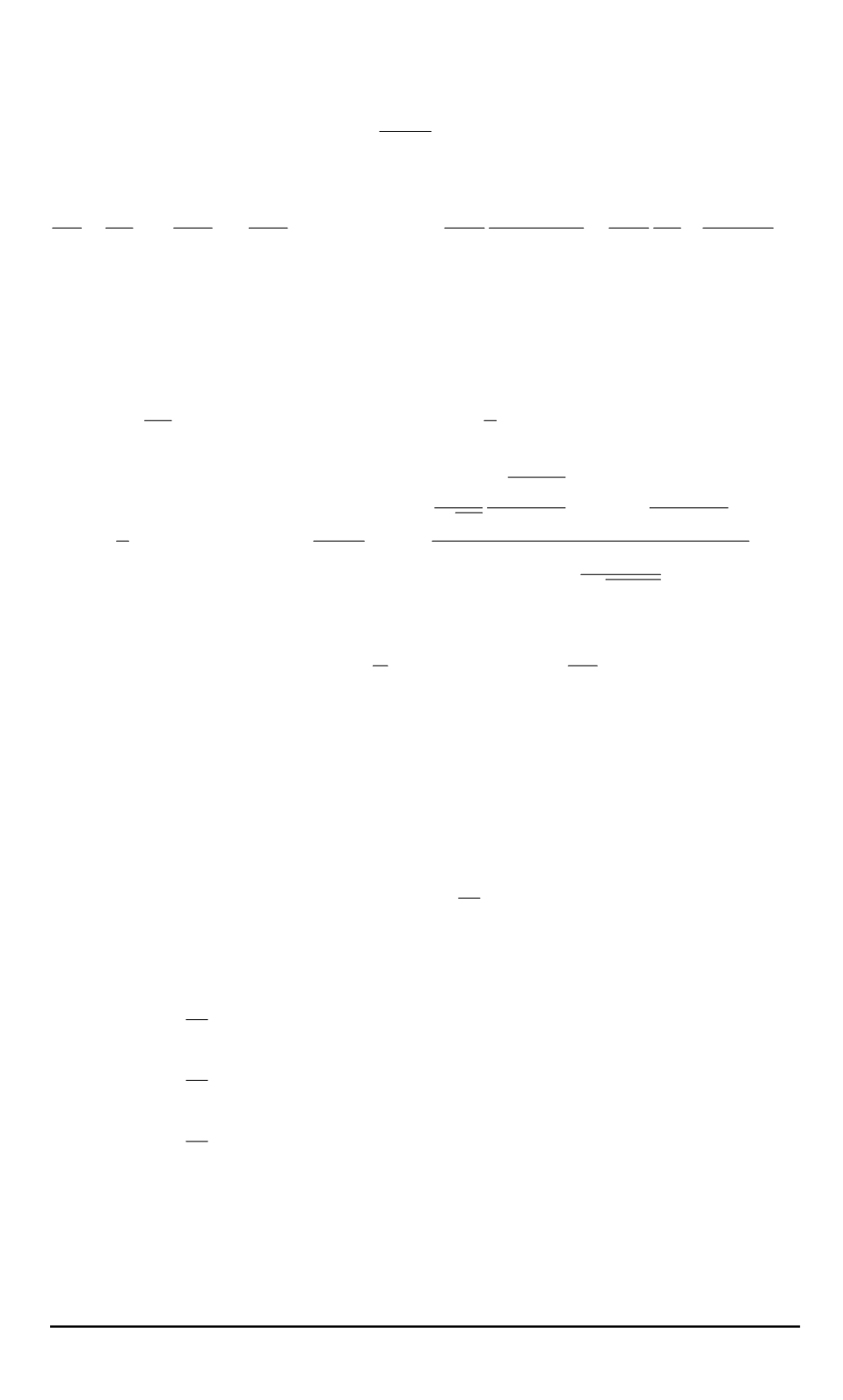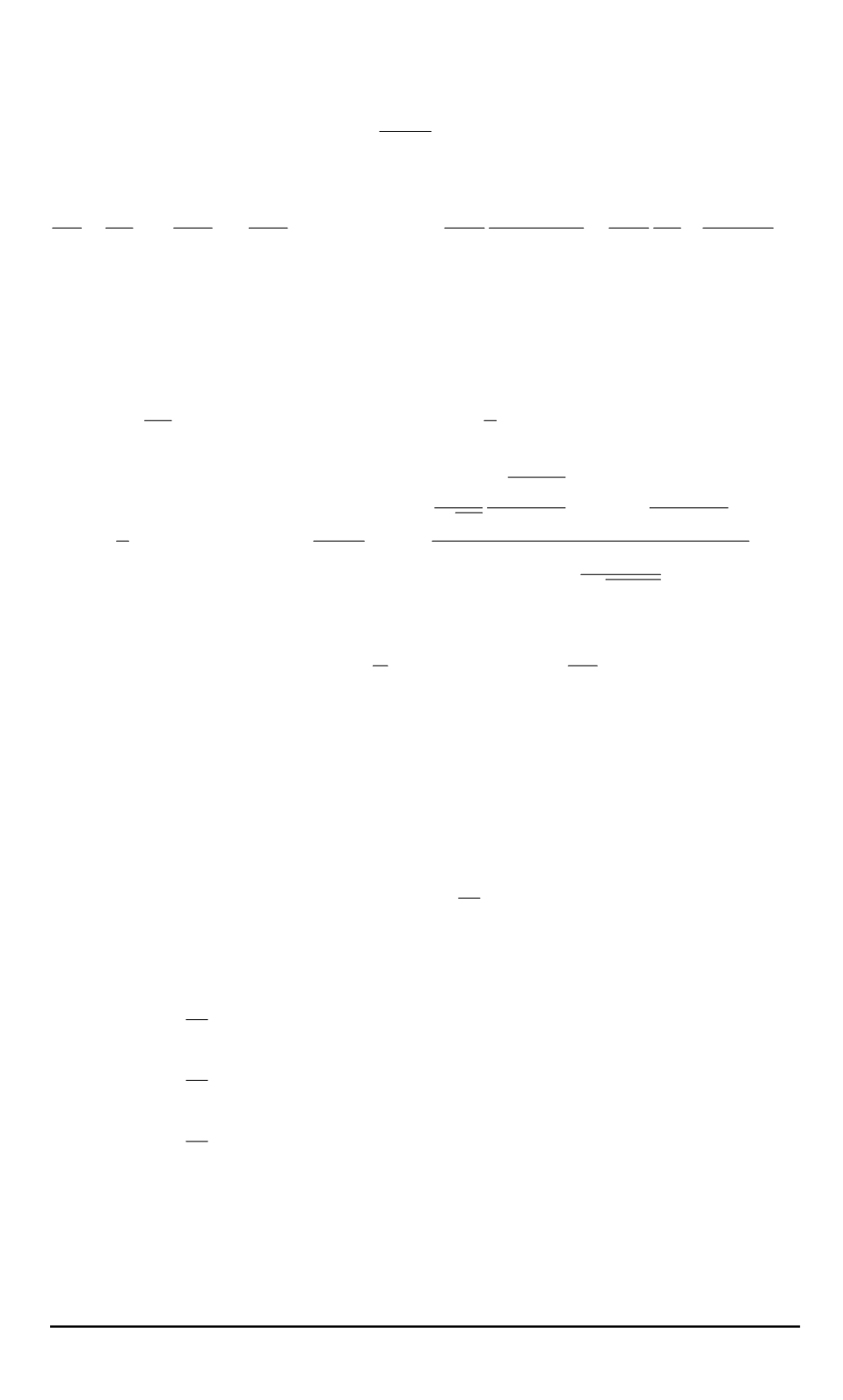
В этом случае при усреднении по
ϕ
правомерно считать, что плот-
ность распределения
f
(
а
, ϕ, t
)
является только функцией амплитуды
и времени, т.е.
f
(
а
, ϕ, t
)
≈
f
(
a, t
)
2
π
.
Тогда
∂f
∂t
≈
∂
∂a
K
д0
2
a
+
K
д1
8
a
3
f
(
a, t
) +
S
2Ω
2
∂
2
f
(
a, t
)
∂a
2
−
S
4Ω
2
∂
∂a
f
(
a, t
)
a
.
Очевидно, что если
K
д1
>
0
, то распределение
f
(
a, t
)
будет стре-
миться к стационарному распределению
f
(
a
)
. Имея в виду уравнения
(9), стохастические характеристики угла
δ
Σ
можно определить как
Д
δ
Σ
=
1
2
π
∞
Z
0
f
(
a
)
2
π
Z
0
cos
ϕdϕ a
2
da
=
1
2
Д
a
=
=
1
2
∞
Z
0
f
(
a
)
a
2
da
=
−
2
K
д0
K
д1
1 +
1
√
2
π
√
K
д
1
S
2Ω
K
д0
exp
−
2Ω
2
K
2
д0
SK
д1
1
−
Φ
2Ω
K
д0
p
K
д1
S
;
f
(
|
δ
Σ
|
> δ
пр
) =
2
π
∞
Z
δ
пр
f
(
a
) arccos
δ
пр
δ
Σ
da.
Анализ правомерности принятия гипотезы о нормальном законе
распределения для рассматриваемого достаточно общего случая, а так-
же пределов ее применимости проводят, исходя из следующих сообра-
жений.
Используя в отношении (8) корреляционный метод расчета, полу-
чаем при введении обозначений:
ω
δ
=
d
dt
δ
Σ
(
t
)
;
Д
δ
Σ
= ˜
δ
2
Σ
;
K
δ
Σ
ω
δ
= ˜
δ
Σ
ω
δ
;
Д
ω
δ
=
ω
2
δ
— приближенные уравнения для определения изменений вто-
рых моментов по времени (знак “
Σ
” опущен для упрощения записи):
d
dt
Д
δ
= 2
K
δω
;
d
dt
K
δω
=
Д
ω
−
Ω
2
Д
δ
−
K
д0
K
δω
−
K
д1
˜
δ
3
ω
δ
;
d
dt
Д
ω
=
−
2Ω
2
K
δω
−
2
K
д0
Д
ω
−
2
K
д1
˜
δ
2
ω
2
δ
+
S.
Отметим, что при
K
δω
= 0
дисперсия угла
δ
Σ
становится посто-
янной
(
Д
δ
=
const
)
, а его численное значение будет определяться из
условия (при
˜
δ
2
ω
2
δ
≈
Д
δ
Д
ω
)
2
Д
ω
(
K
д0
+
K
д1
Д
δ
) =
S
(Ω)
,
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 1 39