щади сечения между частями, зависящего не только от координаты
z
,
но и от времени (см. рис. 2). Поэтому исходная конструкция разби-
вается на две независимые части — правую и левую, имеющие один
общий узел (см. рис. 2). Левая часть описывает характеристики рабо-
чего вещества в канале I, правая — в канале II.
Первая часть задачи посвящена исследованию нагнетания рабоче-
го вещества в полости поршней (движение из канала I в канал II).
В этом случае левую часть можно представить как цилиндрический
канал, расположенный до разрыва площади сечения, правую – как
расположенные после разрыва конический и примыкающий к нему
цилиндрический каналы.
Режим течения рабочего вещества рассчитывается с помощью
двухшаговой схемы Лакса–Вендроффа “предиктор-корректор”, при-
чем этап предиктор выполняется независимо для обеих частей, а на
этапе корректор совместно уточняются значения давления, скорости,
энергии и плотности в общем узле 1.
Численная реализация алгоритма проводится в нормированных пе-
ременных:
z
=
z
S
max
;
S
(
z
) =
S
(
z
)
S
max
,
где
S
max
— максимальная площадь сечения правого канала.
Под относительной площадью отверстия понимается нормирован-
ная площадь сечения между левой и правой частями
S
0
(
t
) =
S
0
(
t
)
S
max
(
S
0
(
t
)
— площадь отверстия, единственного во всей конструкции се-
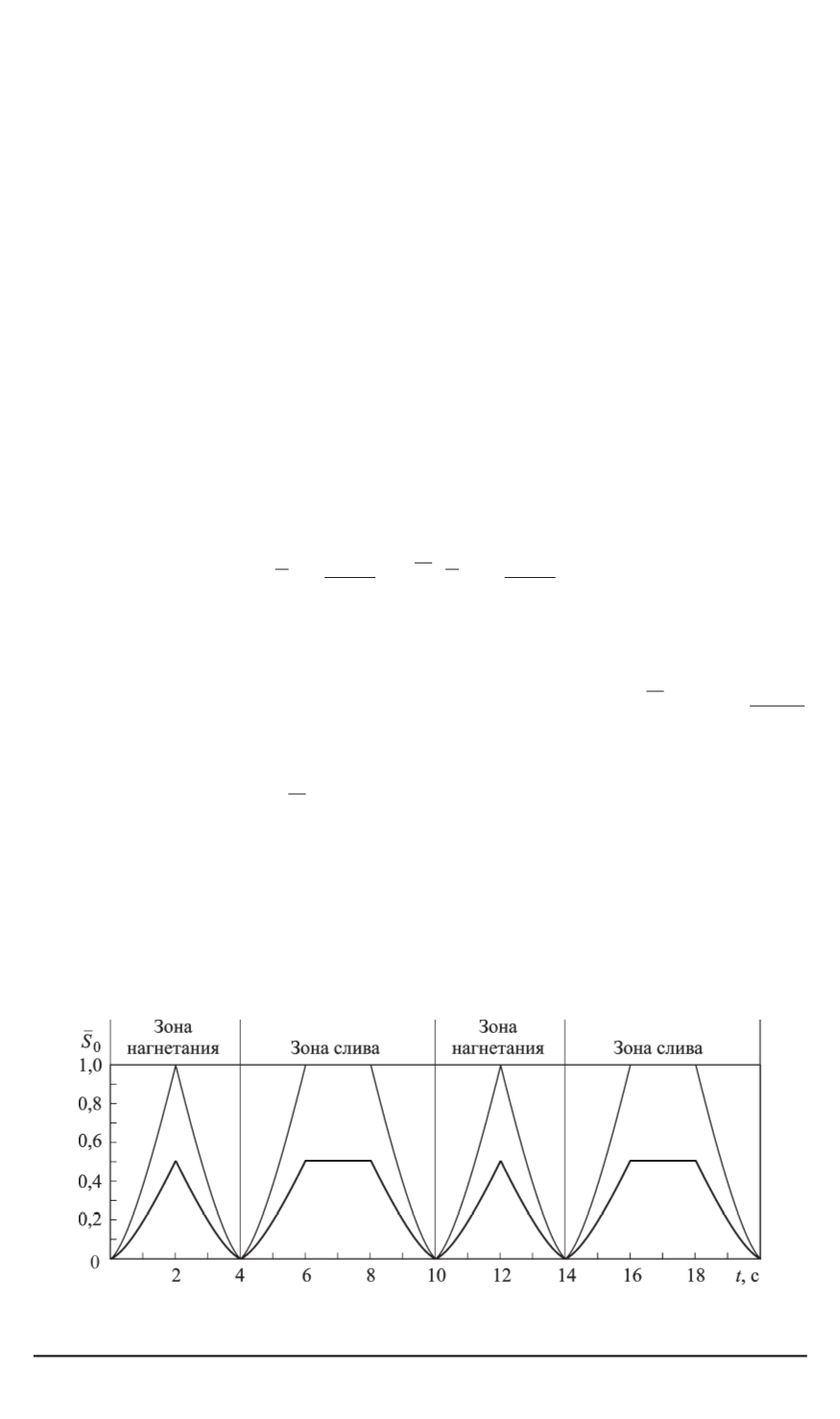
чения). На рис. 3 приведен закон изменения относительной площади
отверстия по времени
S
0
(
t
)
. Верхней кривой соответствует канал II,
выполненный в форме цилиндра. В этом случае максимальное зна-
чение площади отверстия
S
0
(
t
)
равно
S
max
и максимальное значе-
ние относительной площади отверстия равно единице. С увеличением
радиуса цилиндрической части канала II максимальное значение от-
носительной площади отверстия уменьшается (нижние графики, см.
рис. 3).
Рис. 3. Изменение относительной площади сечения между левой и правой час-
тями при различных соотношениях максимальных радиусов каналов I и II
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 4 101


