жений при решении контактной задачи эти напряжения задавали в
ANSYS как начальные посредством использования функции
inis
.
В процессе численного счета задавали различные значения усилий
противоизгиба и определяли погрешностьтолщины листа, которую
рассчитывали по формуле
δ
= 2Δ
v/t,
(12)
где
Δ
v
— максимальная разность радиальных перемещений узлов,
расположенных на рабочей поверхности валка, в зоне контакта с про-
катываемым металлом;
t
— толщина листа (3 мм).
Вначале задавали усилие противоизгиба, рассчитанное по формуле
(7). Результаты численного расчета показали, что разнотолщинность
листа в этом случае составляет
∼
3%. Далее увеличивали усилия про-
тивоизгиба и анализировали значение разнотолщинности. Численный
расчет показал, что наименьшая разнотолщинность листа возникает
при усилиях противоизгиба, составляющих 7% усилия прокатки. На
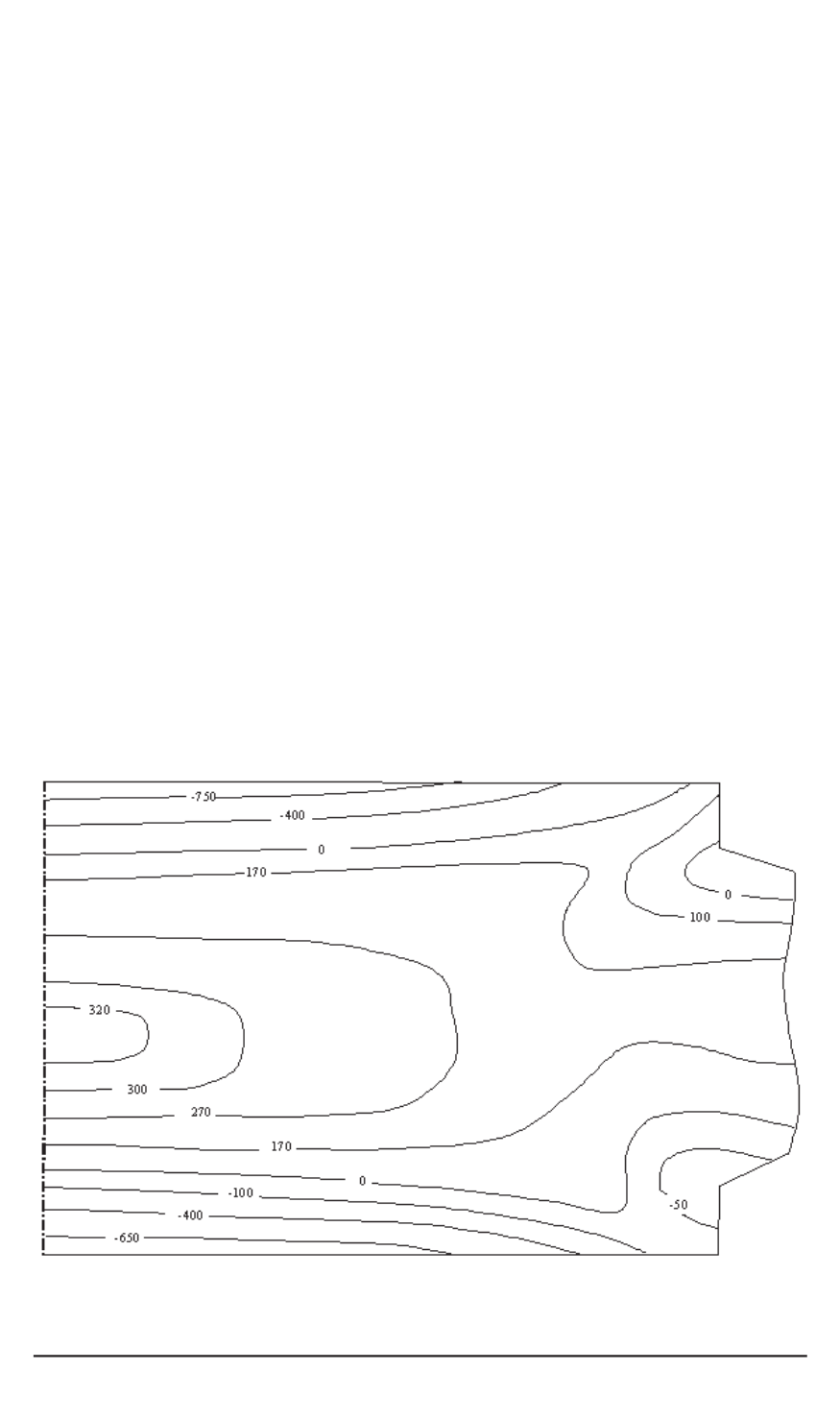
рис. 5 приведены изолинии наиболее опасных осевых напряжений для
этого случая. Из сопоставления рис. 3 и 5 следует, что остаточные
термонапряжения в валках значительно больше эксплуатационных на-
пряжений от прокатки.
Выводы.
1. Приближенное аналитическое решение, основанное
на балочной схеме, дает существенно заниженные значения усилий
противоизгиба.
Рис. 5. Изолинии суммарных осевых напряжений (МПа) от термообработки
и прокатки в рабочем валке с рациональными значениями усилий противо-
изгиба
52 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1


