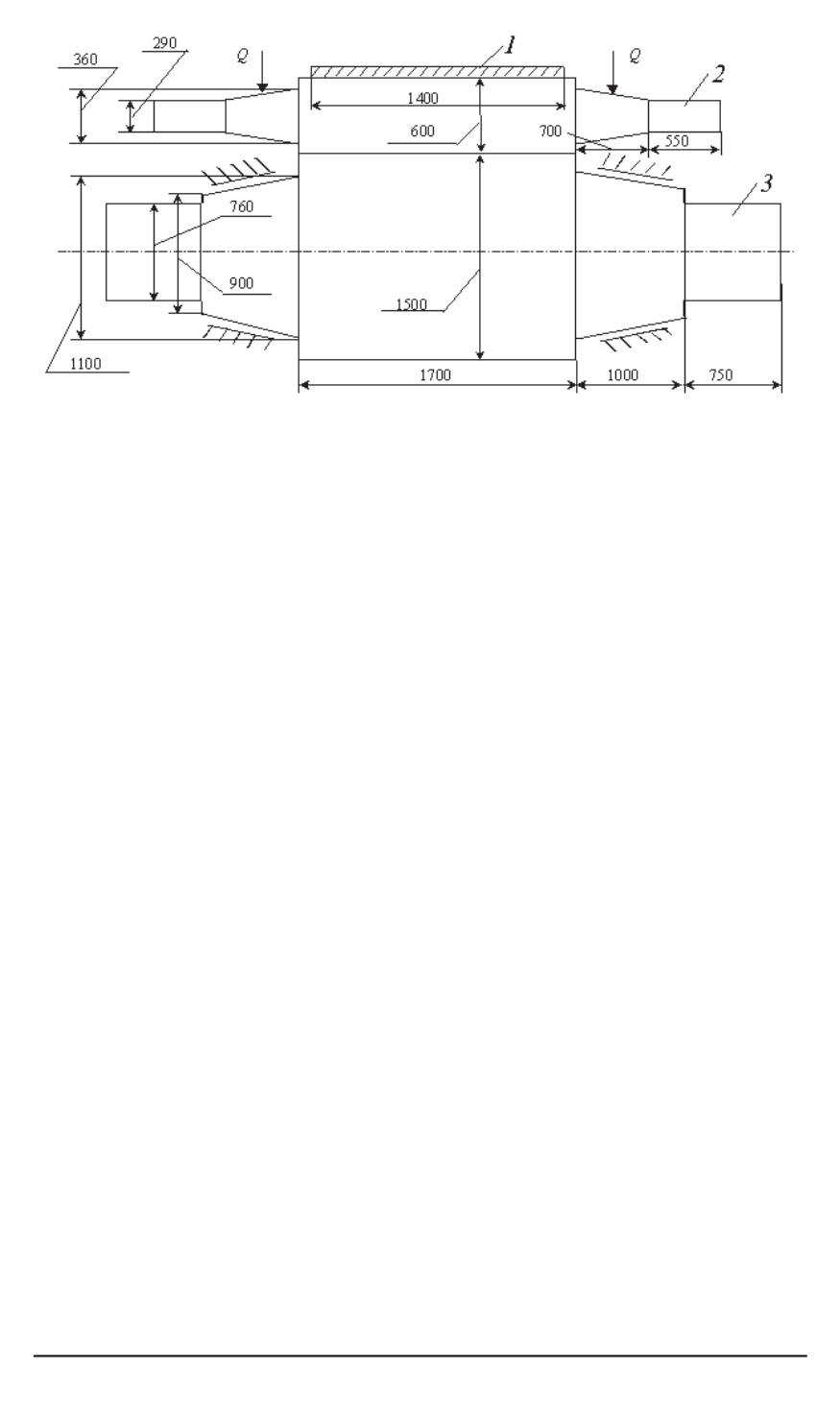
Рис. 1. Схеманижней половины станаКВАРТО 600/1500
×
1700:
1
— прокатываемый лист;
2, 3
— рабочий и опорный валки;
Q
— усилие противоизгиба
возникающие при прокатке [2], поэтому для адекватного определения
усилий противоизгиба необходимо учитыватьв расчете значения этих
остаточных напряжений.
Для обоснования целесообразности применения разработанной ма-
тематической модели были сопоставлены значения усилий противо-
изгиба, полученные путем численного эксперимента, и значения, най-
денные по традиционной методике [1], основанной на балочной схе-
ме. В качестве объекта исследования выбран холоднолистовой четы-
рехвалковый прокатный стан КВАРТО 600/1500х1700, состоящий из
двух рабочих (сталь90ХФ, диаметр 0,6 м, длина рабочей части 1,7 м)
и двух опорных валков (сталь90Х, диаметр 1,5 м, длина рабочей ча-
сти 1,7 м). Усилие прокатки принималосьравным 20МН, а ширина
прокатываемого листа — 1,4 м. Остальные геометрические размеры,
используемые в расчете, приведены на рис. 1. В силу симметрии зада-
чи относительно прокатываемого листа на рисунке изображена только
нижняя частьклети.
Согласно традиционной методике [1] рабочий валок рассматрива-
ется как балка с постоянным поперечным сечением. Дифференциаль-
ное уравнение упругой линии
v
(
z
)
балки в общем случае имеет вид
EI
x
v
IV
(
z
) =
f
(
z
)
,
(1)
где
f
(
z
)
— функция изменения поперечной погонной нагрузки по дли-
не балки;
E
— модульЮнга;
I
x
— момент инерции поперечного сече-
ния.
Общее решение этого дифференциального уравнения складывается
из общего решения однородного уравнения при
f
(
z
) = 0
и частного
46 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1


