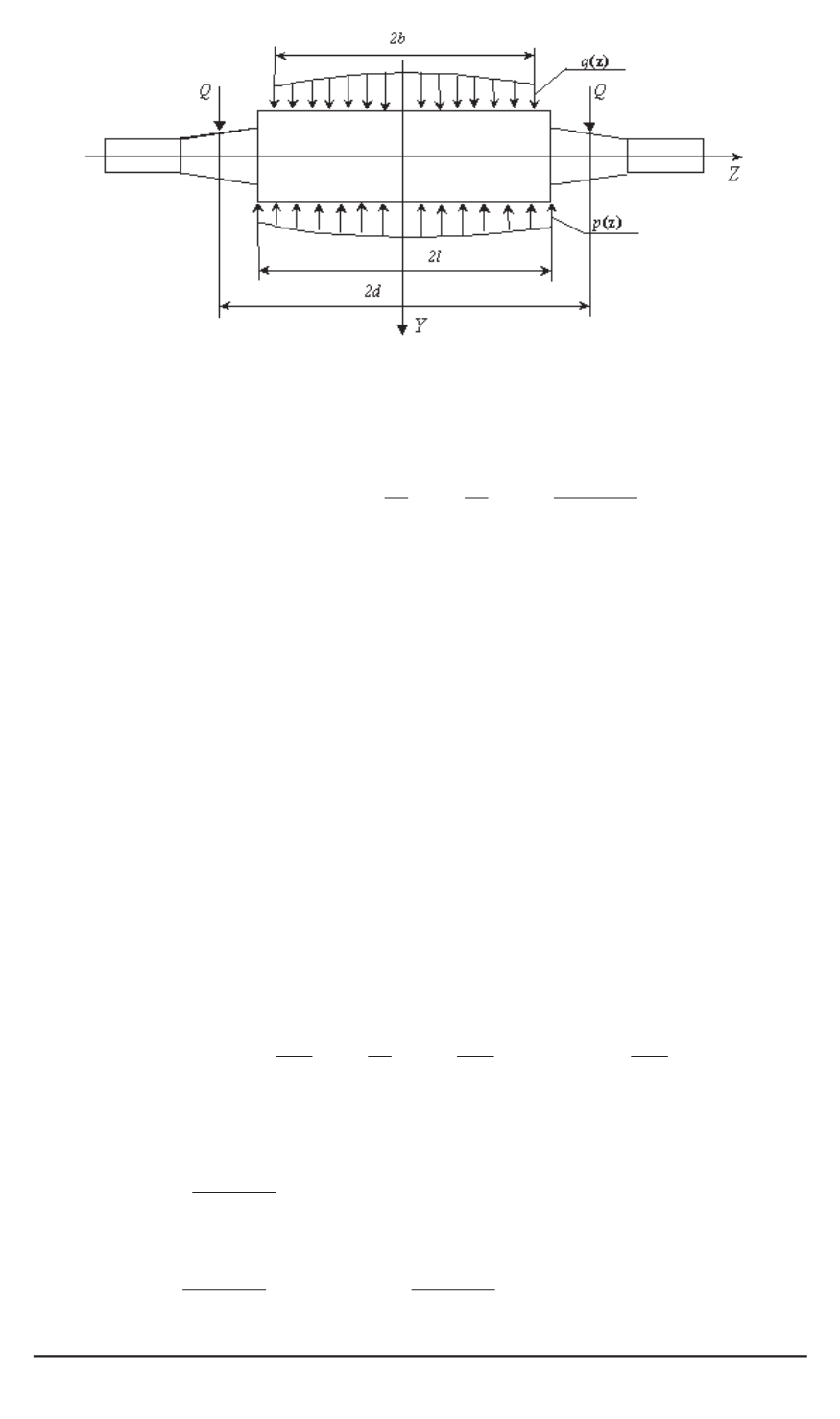
Рис. 2. Силовая схема рабочего валка
решения неоднородного уравнения [3]:
EI
x
v
(
z
) =
c
0
+
c
1
z
+
c
2
z
2
2
+
c
3
z
3
6
+
z
0
(
z
−
t
)
3
6
f
(
z
)
dt,
(2)
где
c
0
, c
1
, c
2
, c
3
— постоянные интегрирования, определяемые гранич-
ными условиями.
Из силовой схемы, приведенной на рис. 2, следует, что функция
f
(
z
)
для рабочего валка имеет следующий вид:
f
(
z
) =
⎧⎨
⎩
0
,
l <
|
z
|
d
;
−
p
(
y
)
,
b <
|
z
|
l
;
q
(
z
)
−
p
(
z
)
,
0
|
z
|
b.
(3)
Рассмотрим граничные условия задачи. Симметрия рабочего валка
относительно срединной плоскости приводит к тому, что в нача-
ле координат угол поворота равен нулю (
v
(0) = 0
); изгибающий
момент в точках приложения усилий противоизгиба также равен
нулю (
v
(
±
d
) = 0
), а поперечные силы — равны этим усилиям
(
EI
x
v
(
±
d
) =
Q
). С учетом граничных условий выражение для
прогиба валка (2) принимает вид
EI
x
v
(
z
) =
c
0
+
Q
z
2
d
2
+
Q
z
3
6
+
0
−
l
z t
2
2
p
(
z
)
dt
+
0
−
b
z t
2
2
q
(
z
)
dt
+
+
⎧⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
0
,
l <
|
z
|
d
;
−
z
−
l
(
z
−
t
)
3
6
p
(
z
)
dt,
b <
|
z
|
l
;
l
−
b
(
z
−
t
)
3
6
q
(
z
)
dt
−
z
−
l
(
z
−
t
)
3
6
p
(
z
)
dt,
0
|
z
|
b.
(4)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1 47


