
Численное моделирование прецессии упругой волны в цилиндрическом резонаторе…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 5
47
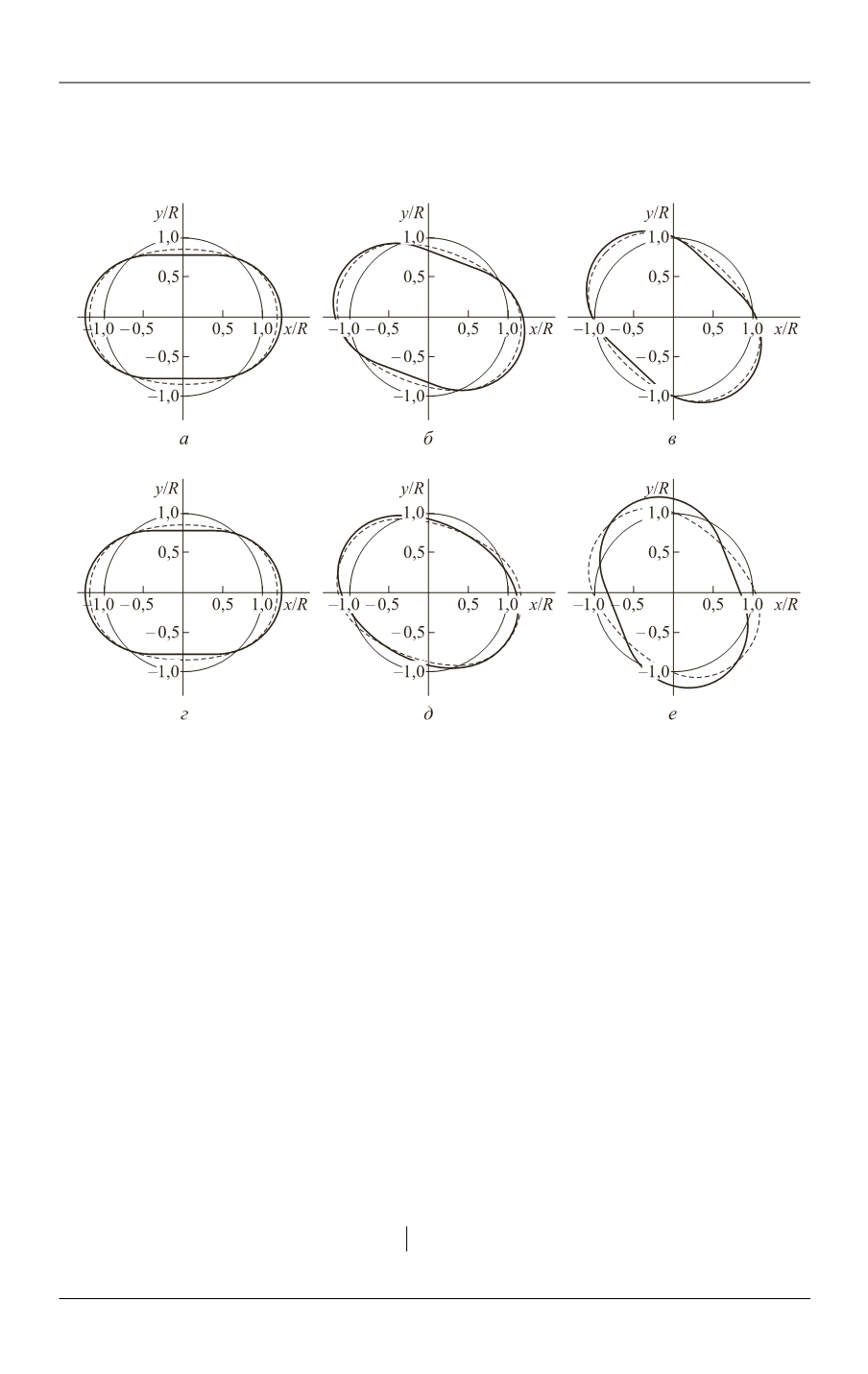
Решение, представленное формулой (12), для оболочки без дефекта (
= 0)
описывает всего лишь эффект Брайана, что видно по положению упругой вол-
ны в равноотстоящие моменты времени (рис. 3,
а
,
б
,
в
).
Рис. 3.
Положение упругой волны при
s
=
l
/
2 в моменты времени
t
= 0,
t
= 400 /
f
2
,
t
= 800 /
f
2
(
а
,
б
,
в
— дефект отсутствует;
г
,
д
,
е
— параметр дефекта
= 2∙10
–3
)
Для сравнения на рис. 3 штриховой линией в несколько отличном масштабе
показано теоретическое решение, т. e. график функции cos (2(φ +
K
t
)). Численное
решение показывает, что в системе координат, связанной с корпусом, упругая вол-
на прецессирует относительно него с постоянной угловой скоростью
K
в направлении, противоположном вращению корпуса.
В случае наличия дефекта
= 2∙10
–3
упругая волна прецессирует неравно-
мерно (рис. 3,
г
,
д
,
е
) и при этом опережает теоретическое решение.
Знание параметра дефекта плотности
= 2∙10
–3
выбрано довольно большим
для того, чтобы повысить наглядность рисунка. При меньших значениях пара-
метра
разность в положении овалов, изображенных штриховой и сплошной
линиями, будет практически незаметна. Поэтому при меньших значениях де-
фекта вычисляли угловое положение экстремума функции
w
через целое число
периодов колебаний и сравнивали его с теоретическим, т. e. уход гироскопа по
найденному решению (12) был рассчитан следующим образом:
max
.
w
K t
(14)
















