
И.Ф. Кобылкин, А.А. Горбатенко
64
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 6
большие перенапряжения (эффект концентрации напряжений), которые и обу-
словливают распространение трещин и разрушение образцов при сравнительно
небольших нагрузках. При сжатии сжимающие силы в отличие от растягиваю-
щих могут передаваться через существующие трещины, не приводя к концен-
трации напряжений [5].
Таблица 1
Физико-механические характеристики некоторых керамик
Материал
Плот-
ность
ρ, г/см
3
Модуль
упруго-
сти
Е
, ГПа
Началь-
ная твер-
дость
керамики
Коэф-
фициент
Пуас-
сона,
Продоль-
ная ско-
рость
звука
c
к
, км/с
Предел прочности, МПа, при
растя-
жении
σ
р
сжатии
σ
сж
изгибе
σ
изг
Корунд
Al
2
O
3
3,9
407
HV 18,0
(HRA 90)
0,22
10,4
260
2000–3000 220 ±
20
Карбид
бора В
4
С 2,4…2,5
475
До HV 28
(HRA 96)
0,2
12,4
–
≥ 2500
420 ±
20
Карбид
кремния
SiC
3,0
350 ±
20
HV 20
(HRA 93)
0,17
10,5
–
≥ 2500
350 ±
20
Для определения взаимосвязи между прочностными характеристиками ке-
рамики и углом раствора конуса сравним силы, необходимые для выбивания из
слоя керамики конической пробки и срезания цилиндрической пробки. Схема
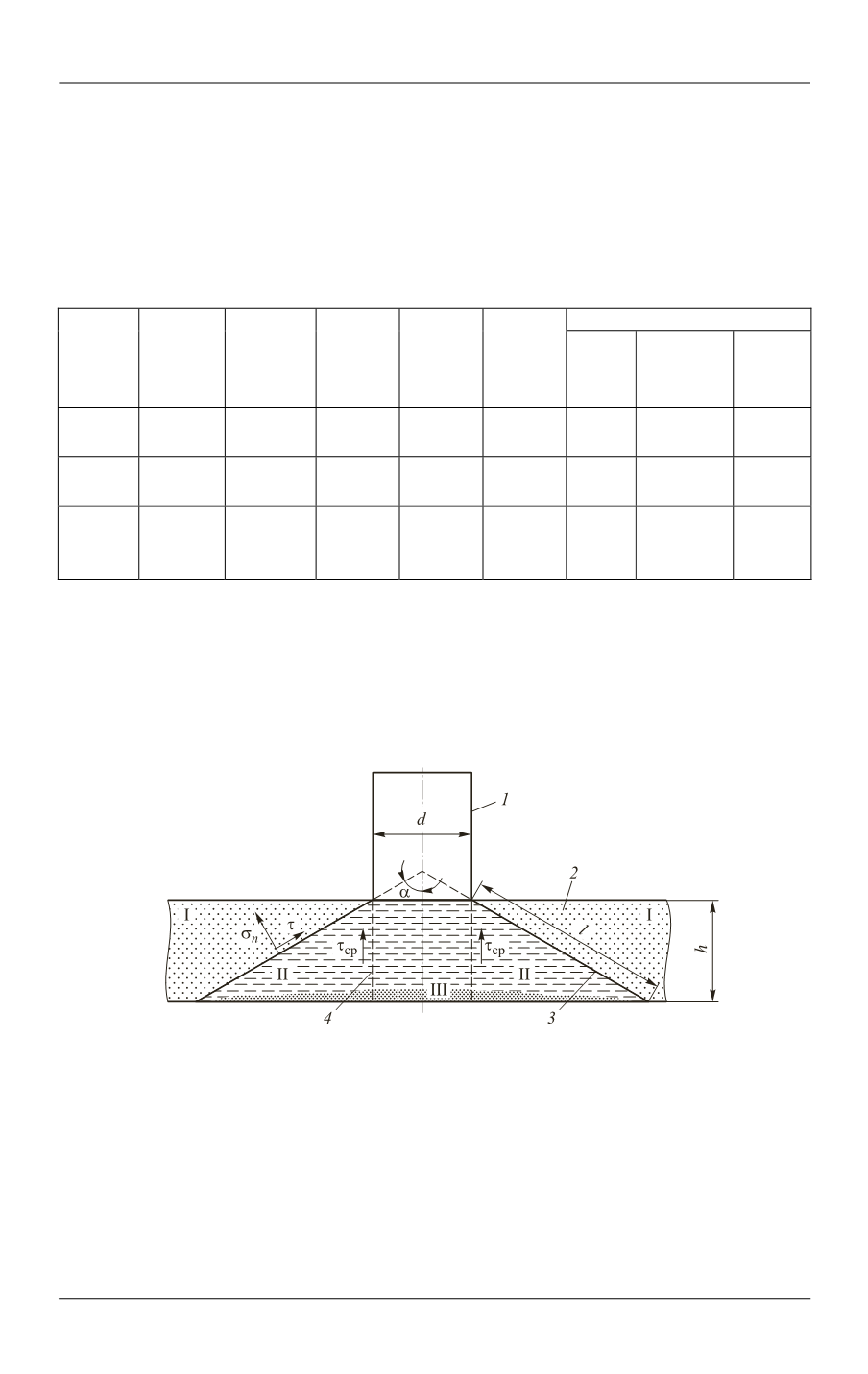
взаимодействия ударника диаметром
d
с керамической преградой толщиной
h
приведена на рис. 2. Сила
F
ср
, необходимая для срезания цилиндрической проб-
ки высотой
h
и диаметром
d
, равна произведению сдвиговой прочности τ
ср
материала преграды на площадь боковой поверхности пробки:
ср ср
F
dh
.
(1)
Рис. 2.
Расположение конической и цилиндрической трещин при пробивании
керамической преграды:
1
— ударник;
2
— керамическая преграда;
3
— коническая трещина отрыва;
4
— цилиндрическая
трещина среза. I, III — области, в которых действуют растягивающие напряжения; II — область,
в которой действуют сжимающие напряжения
















