
Шапиро – Уилка. Из теоретической статистики известно, что
H
0
рас-
сматриваются принятыми, если подтверждается неравенство:
α
l
>
0
,
5
(табл. 2).
Нормальные распределения имеют место только в четырех случаях
шлифования (подчеркнутые значения, см. табл. 2) из 20. В условиях
нарушений однородности и нормальности распределений эксперимен-
тальных данных оправданным оказалось привлечение непараметриче-
ского (в частности рангового) метода статистики. В этом случае к
входным данным относятся два параметра: (3) и (6), значения которых
по результатам эксперимента и их статистической обработки приведе-
ны в табл. 3.
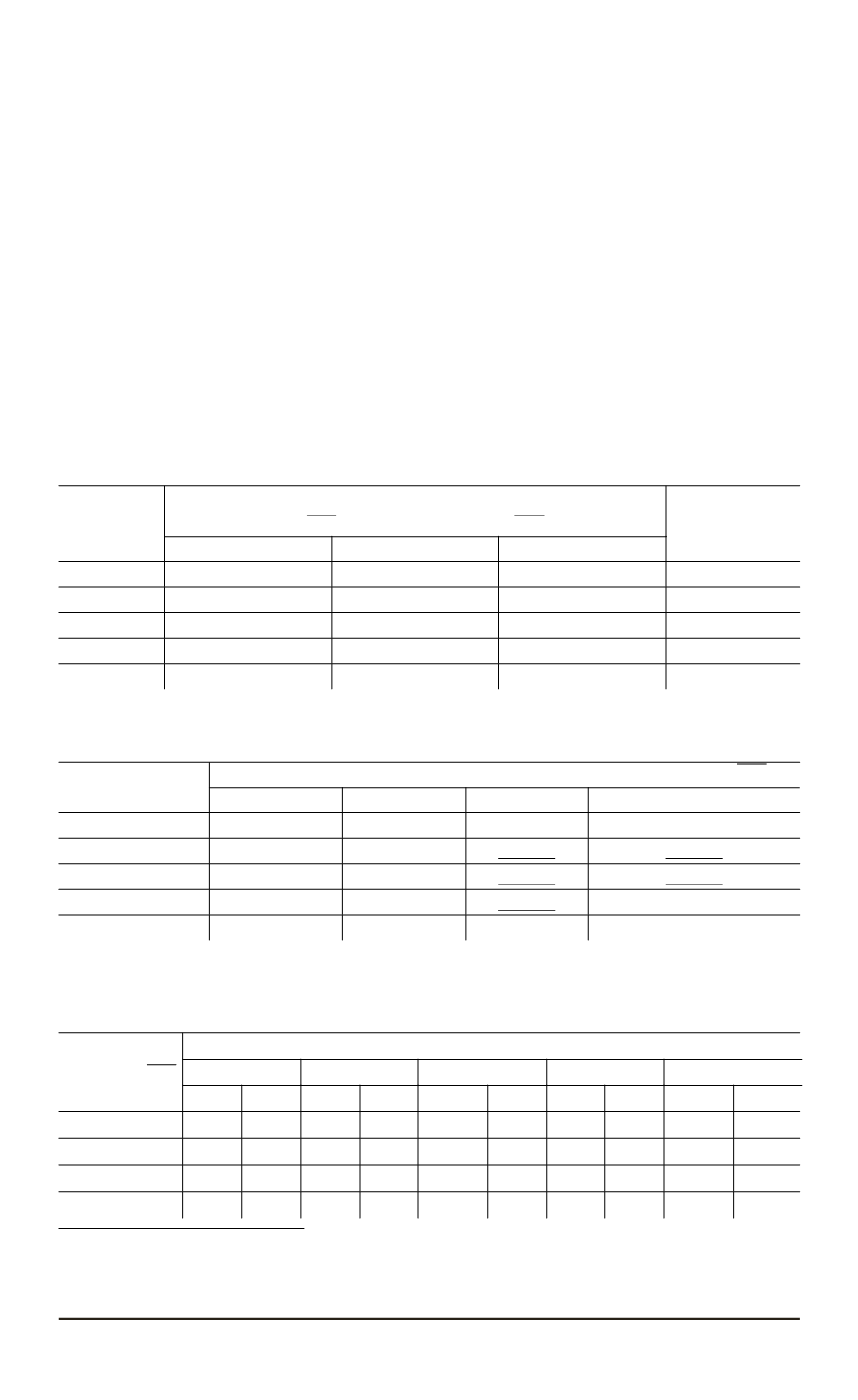
Таблица 1
Проверка однородности дисперсий при принятом уровне значимости
α
m
= 0
,
05
Параметр
Расчетные уровни значимости
α
m
для множеств
l
= 1; 4
по критериям
m
= 1; 3
Принятие
H
0
1
2
3
R
a
1
0,999
1,000
0,999
–
R
z
1
1,000
1,000
1,000
–
R
max1
0,991
0,999
0,996
–
S
1
0,995
0,576
0,563
–
S
m
2
0,998
0,925
0,772
–
Таблица 2
Проверка нормальности распределений по критерию Шапиро – Уилка
Параметр
Расчетный уровень значимости
α
l
при переменных
l
= 1; 4
1
2
3
4
R
a
1
0,0100
0,0175
0,2897
0,0184
R
z
1
0,1324
0,0239
0,7746
0,9949
R
max1
0,1806
0,2968
0,7938
0,8116
S
1
0,00000
0,0032
0,6100
0,0144
S
m
2
0,00005
0,0827
0,0551
0,0129
Таблица 3
Входные данные для исследования влияния зернистости ВПК на качество
шлифованных деталей
Круг
l
= 1; 4
Параметр, мкм
R
a
1
R
max1
S
1
R
z
1
S
m
2
˜
y
КШ
˜
y
КШ
˜
y
КШ
˜
y
КШ
˜
y
КШ
1
0,614 0,07 3,722 0,543 13,192 1,745 2,281 0,266 83,36 28,393
2
0,584 0,119 3,325 0,443 13,145 1,618 2,122 0,205 96,746 57,239
3
0,602 0,27 3,584 1,271 13,395 2,071 2,241 0,955 84,909 48,243
4
0,565 0,11 3,369 0,788 12,755 1,514 2,118 0,423 80,519 36,885
П р и м е ч а н и е. В табл. 1–3 круги CBN30 100 OVK27-КФ40
l
: 1 — B76, 2 — B107,
3 — B126, 4 — B151.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 6 101
















