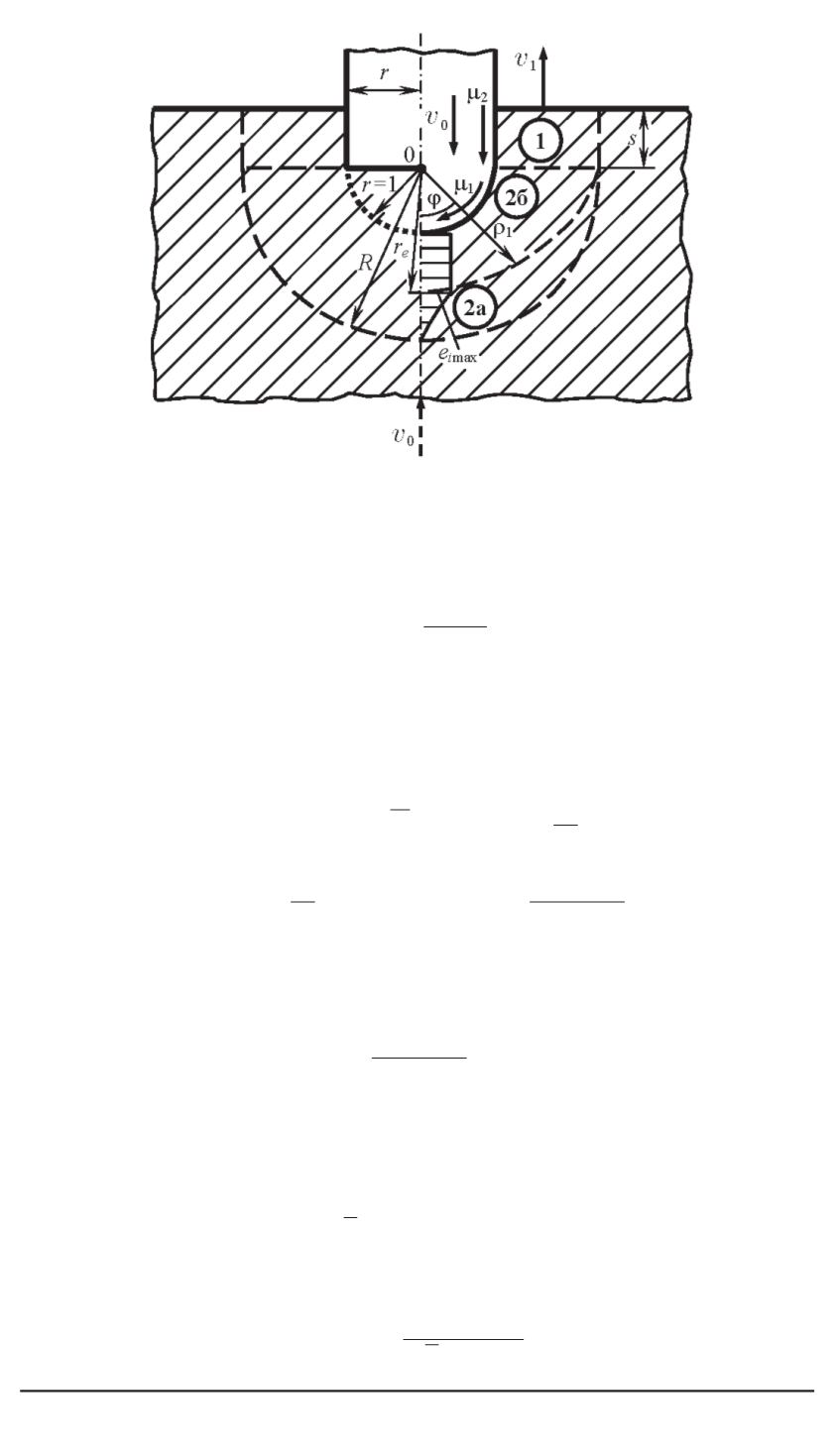
Рис. 1. Расчетная схема вдавливания пуансона с плоским (слева) или сфериче-
ским (справа) торцом в полупространство
Решение такого уравнения, как известно, имеет вид [3, с. 36]
F
(
ρ
) = Φ(
ρ
)
Φ
2
(
ρ
)
Φ(
ρ
)
dρ
+
C
1
,
(16)
где
Φ(
ρ
) =
e
−
Φ
1
(
ρ
)
dρ
.
С учетом этого можно записать
Φ(
ρ
) =
e
−
2
dρ
ρ
=
e
−
2 ln
ρ
=
1
ρ
2
,
(17)
F
(
ρ
) =
1
ρ
2
C dρ
+
C
1
=
Cρ
+
C
1
ρ
2
.
(18)
Подставив функцию (18) в равенство (33) из работы [1], найдем
касательное напряжение
τ
ρϕ
=
Cρ
+
C
1
ρ
2
sin
ϕ.
(19)
Произвольные постоянные определяем из граничных условий
(рис. 1)
τ
ρϕ
=
μ
1
σ
s
при
ϕ
= 90
◦
и
ρ
= 1;
τ
ρϕ
=
−
σ
s
/
√
3
при
ϕ
= 90
◦
и
ρ
=
R,
с учетом которых
C
=
−
σ
s
R
2
+ 2
μ
1
√
3(
R
−
1)
;
(20)
ISSN 0236-3941. ВестникМГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 3 49


