
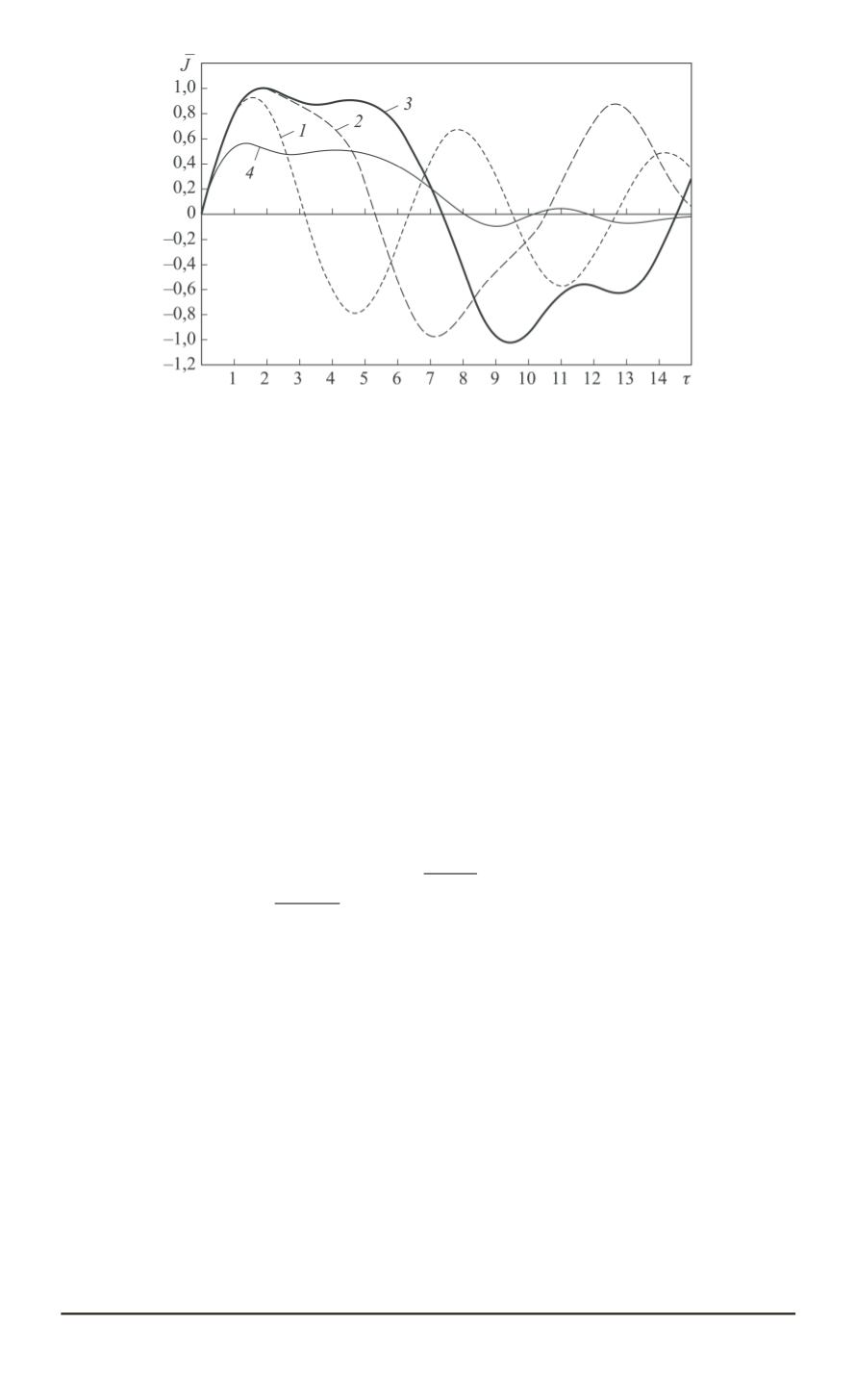
Рис. 2. Зависимость безразмерного тока от безразмерного времени для
A
= 0
,
1
,
θ
= 0
,
01
:
1
—
n
= 1
,
ε
= 0
,
1
;
2
—
n
= 2
,
ε
= 0
,
1
;
3
—
n
= 3
,
ε
= 0
,
1
;
4
—
n
= 3
,
ε
= 1
Следует обратить внимание на то, что безразмерные комплексные
параметры
А
и
ε
определяются по емкости
C
0
одиночного звена фор-
мирующей линии.
Система уравнений (6) решалась численно при вариации безраз-
мерных критериев в диапазонах:
A
= (0
,
01
. . .
10)
,
ε
= (0
,
01
. . . ,
2)
,
θ
= (0
,
01
. . .
1)
.
Результаты расчета.
На рис. 2 приведены зависимости безразмер-
ного тока разряда
˜
J
от безразмерного времени
τ
при вариации чи-
сла звеньев
n
емкостной формирующей линии от одного до трех.
Видно, что уровень максимального тока
f
J
m
и время его достиже-
ния
τ
m
≈
1
,
5
практически не зависят от
n
. Параметр
f
J
m
зависит
от декремента затухания
ε
и приближенно может быть аппроксими-
рован зависимостью
f
J
m
= exp(
−
0
,
7
ε
)
. Размерные значения времени
возрастания тока разряда (
≈
1
,
5
√
L
0
C
0
) и уровня его максимального
значения (
≈
f
J
m
U
0
p
C
0
/L
0
) определяются параметрами первого звена
формирующей линии.
Увеличение числа звеньев
n
формирующей линии при прочих рав-
ных условиях ведет к увеличению длительности первого полупериода
тока
τ
1
/
2
. Так, для трехзвенной линии
τ
1
/
2
≈
7
, а для двухзвенной —
τ
1
/
2
≈
5
. Увеличение декремента затухания
ε
несколько увеличивает
длительность первого полупериода тока.
Здесь также отметим, что параметры
А
и
θ
на ток разряда не ока-
зывают заметного влияния. Так, увеличение
θ
от 0,01 до 1 приводит к
незначительному (до 10. . . 20%) снижению тока разряда.
В зависимости от значений параметров
А
,
ε
и
θ
возможна реализа-
ция двух различных режимов ускорения формируемого плазменного
образования.
92 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 4

















