
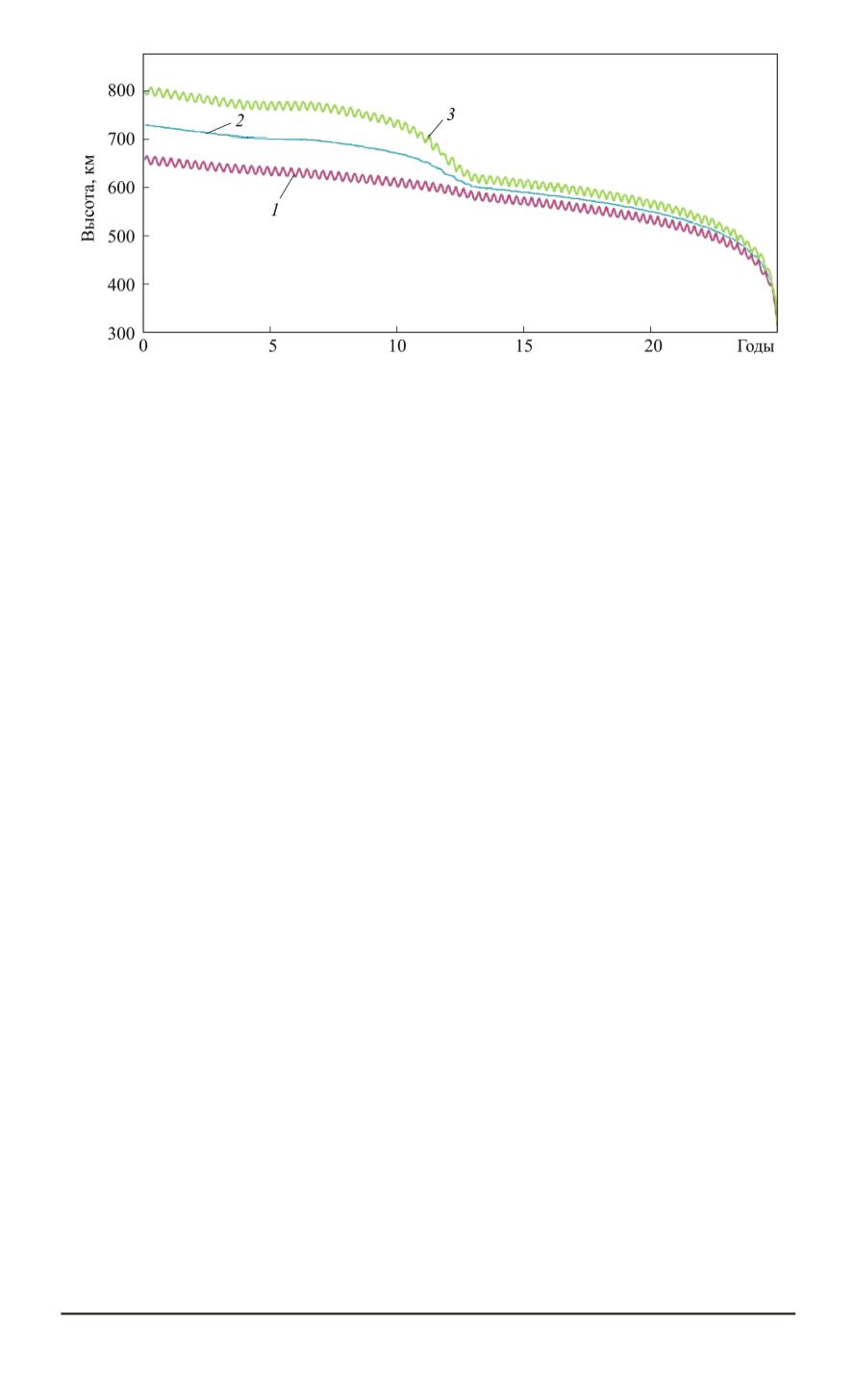
Рис. 3. Падение высоты в течение 25 лет при наклонении 98
◦
(начальная
верхняя высота 800 км):
1
— высота в перигее;
2
— средняя высота;
3
— высота в апогее
поиска орбиты захоронения КА для точно (менее одного часа) за-
данного интервала времени существования использует экстраполятор
TRACE, основанный на численно-аналитической теории THEONA.
Входные данные итерационной процедуры следующие:
— параметры начальной орбиты КА (большая полуось
a
, эксцен-
триситет
e
, наклонение
i
, аргумент перигея
ω
, долгота восходящего
узла
Ω
, начальный момент времени
t
0
и аргумент широты
u
0
) и харак-
теристики самого КА (масса, баллистический коэффициент и коэффи-
циент отражения солнечных лучей — светового давления);
— продолжительность интервала времени захоронения
T
L
; КА дол-
жен войти в плотные слои атмосферы (с последующим падением) в
заданный момент времени с допустимой точностью;
— режим выбора орбиты захоронения: круговая или эллиптическая
с фиксированным апогеем. В обоих вариантах сохраняется плоскость
орбиты (наклонение и долгота восходящего узла) на начальный мо-
мент времени.
Для эллиптической орбиты захоронения фиксируется также точка
апогея и высота (геоцентрическое расстояние) апогея. Начальный мо-
мент времени сохраняется. Таким образом, решается граничное урав-
нение
A
h
0
=
h
min
,
где
h
min
— высота входа КА в плотные слои атмосферы Земли;
h
0
=
h
π
(
t
0
)
— высота перигея орбиты захоронения в начальный
момент времени
t
0
;
A
— оператор, зависящий от времени
T
L
суще-
ствования КА на орбите и фиксированных параметров
Q
искомой
орбиты захоронения.
При поиске круговой орбиты захоронения фиксированным параме-
тром орбиты является
Q
=
{
i
0
,
Ω
0
}
(в начальный момент времени
t
0
),
при поиске эллиптической орбиты захоронения —
Q
=
{
h
α
, ω
0
, i
0
,
Ω
0
}
12 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 4

















