
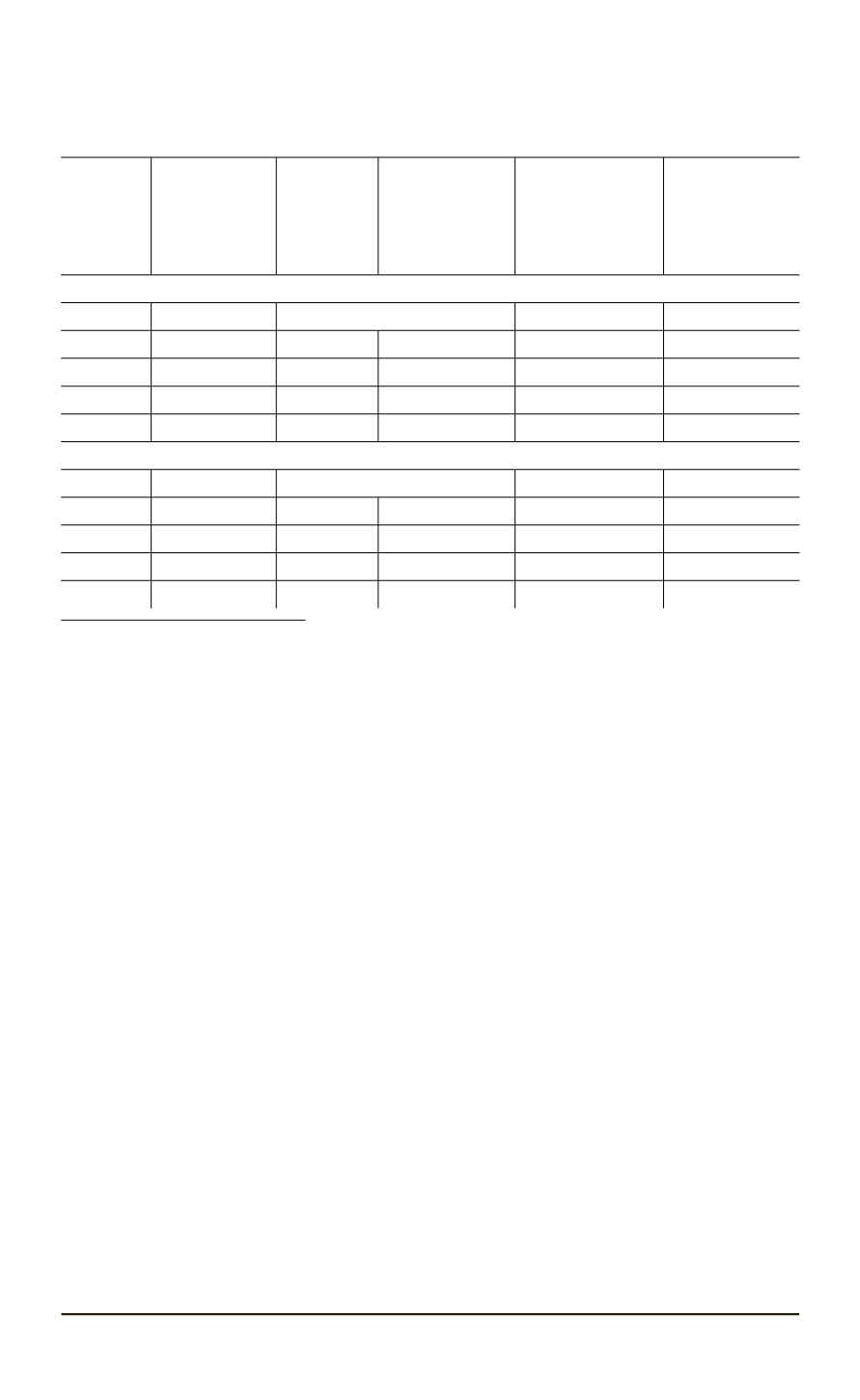
Результаты расчета ошибки эффективности приведены в табл. 3.
Таблица 3
Расчет ошибки эффективности
Скорость
v
, см/c
Расстояние
между
источниками
∗
l
, см
Мощность
лазерного
излучения
Р
л
, кВт
Ошибки рас-
чета мощно-
сти лазерного
излучения
Δ
Р
, кВт
Эффективность
лазерного
воздействия
Э, %
Ошибки
эффективнос-
ти Э, %
Р
=
Р
(1
,
−
0
,
35
)
−
Р
л
Δ
Э
=
Э
−
Э
0
1,0
– 0,35
Р
(1
,
−
0
,
35)
= 0
,
61
Э
0
= 27
1,01
– 0,4
0,63
– 0,02
25
– 2
1,01
– 0,3
0,58
0,03
30
3
0,99
– 0,4
0,62
– 0,01
26
– 1
0,99
– 0,3
0,57
0,04
32
5
Δ
Р
=
Р
(1
,
0
,
1)
−
Р
л
Δ
Э
=
Э
−
Э
0
1,0
0,1
Р
(1
,
0
,
1)
= 0
,
56
Э
0
= 33
1,01
0,15
0,62
– 0,06
26
– 8
1,01
0,05
0,52
0,04
38
5
0,99
0,15
0,62
– 0,06
26
– 8
0,99
0,05
0,51
0,05
39
6
П р и м е ч а н и е.
∗
Знак минус означает, что дополнительный источник теплоты
находится перед лазерным лучом.
Модель прогнозирования эффективности процесса была получена
с помощью метода регрессионного анализа [5]. Это позволяет вы-
полнить оценку коэффициентов и проверку основных статистических
гипотез об уравнении регрессии, его коэффициентах и прогнозируе-
мых значениях отклика. Предполагалось, что отклик (эффективность
воздействия лазерного излучения) связан с параметрами обработки
(факторами) следующим соотношением:
Э
=
b
0
+
b
1
v
+
b
2
l
+
b
3
vl
+
b
4
v
2
+
b
5
l
2
+
b
6
l
2
v
+
b
7
lv
2
,
(2)
где Э — эффективность воздействия лазерного излучения;
b
i
—
i
-й ко-
эффициент уравнения;
v
— скорость обработки;
l
— расстояние между
источниками.
Для получения коэффициентов уравнения (2) используется метод
наименьших квадратов, основанный на минимизации суммы квадра-
тов отклонений значений, предсказанных уравнением (2), от исходных
данных (см. табл. 1, 2). Согласно данному методу вектор-столбец оце-
нок коэффициентов регрессии можно рассчитать по формуле [6]
B
= (
X
T
X
)
−
1
X
T
Э
,
(3)
где
Х
— матрица независимых факторов; Э — вектор эффективности
лазерного воздействия.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 75

















