
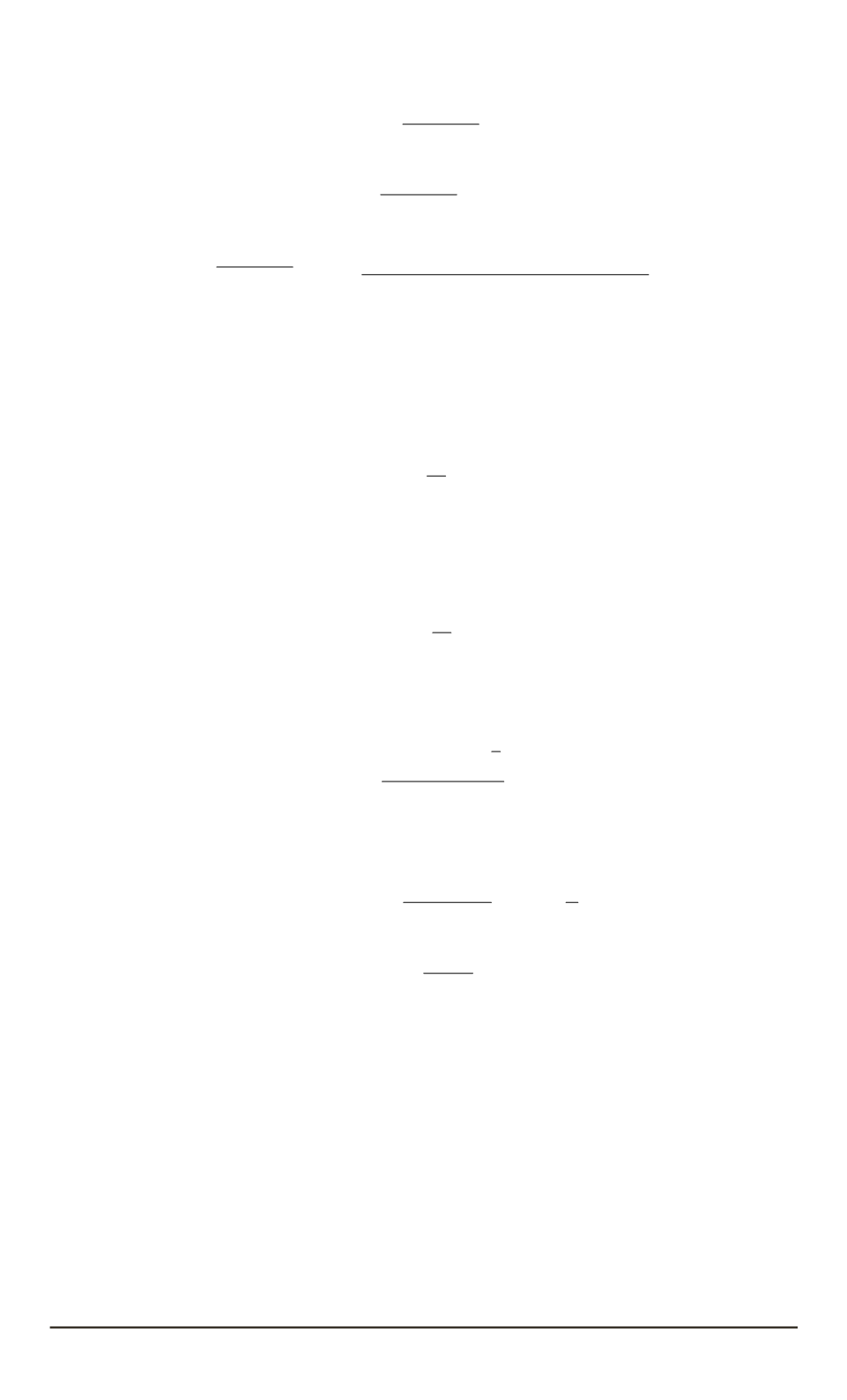
зазора между сопрягаемыми точками взаимно развернутых хорд арок
будет определяться соотношением
Δ
г
з
=
q
x
2
0
+
y
2
0
Δ
ϕ,
(10)
где
Δ
г
з
— значение зазора, а
p
x
2
0
+
y
2
0
— расстояние от рассматривае-
мых точек до начала арок,
q
x
2
0
+
y
2
0
=
r
p
(
t
0
−
sin
t
0
)
2
+ (1
−
cos
t
0
)
2
.
(11)
В момент открытия зазора нормали к сопрягаемым точкам арок
разных зубьев развернутся на разный угол, а в момент закрытия зазора
нормали к сопрягаемым точкам разных арок — совпадут. Уравнение
нормали к циклоиде в локальной системе координат имеет вид [5]
y
−
r
(1
−
cos
t
0
) = tg
t
0
2
[
x
−
r
(
t
0
−
sin
t
0
)]
.
(12)
Для выявления геометрии взаимных положений сопрягаемых арок
циклоид неконтактирующих зубьев используется уравнение касатель-
ной к циклоиде
y
−
r
(1
−
cos
t
0
) = ctg
t
0
2
[
x
−
r
(
t
0
−
sin
t
0
)]
.
(13)
Для расчета контактных напряжений в формуле Герца используется
уравнение радиуса кривизны циклоиды
ρ
=
[1 + (
y
0
x
)
2
]
3
2
y
00
x
.
(14)
Здесь
y
0
x
— первая производная
y
по
x
, а
y
00
x
— вторая производная
y
по
x
:
y
0
x
=
y
0
t
/x
0
t
=
sin
t
1
−
cos
t
= ctg
t
2
;
(15)
y
00
x
=
(
y
0
x
)
0
t
x
0
t
.
(16)
Здесь
x
0
t
и
y
0
t
— производные
x
и
y
по параметру
t
.
Выводы.
Разработана расчетная модель циклоидального зубчато-
го волнового зацепления ВМ. Его основными достоинствами являют-
ся: повышенный КПД, снижение более чем в 2 раза нижней границы
передаточных отношений ВМ и увеличение быстроходности выход-
ного вала, что позволит существенно расширить область применения
ВМ; ожидаемое увеличение нагрузочной способности и усталостного
ресурса ВМ за счет снижения контактных напряжений и напряжений
в концентраторах и их взаимного разнесения; повышение плавности
хода и бесшумности работы.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 2 115

















