
Расчетная схема геометрии волнового зацепления с циклоидальной формой
зубьев колес
удаляются друг от друга. При этом из-за плавности перехода при нуле-
вой производной от головки к впадине зуба существенно снижаются
напряжения и в самих концентраторах.
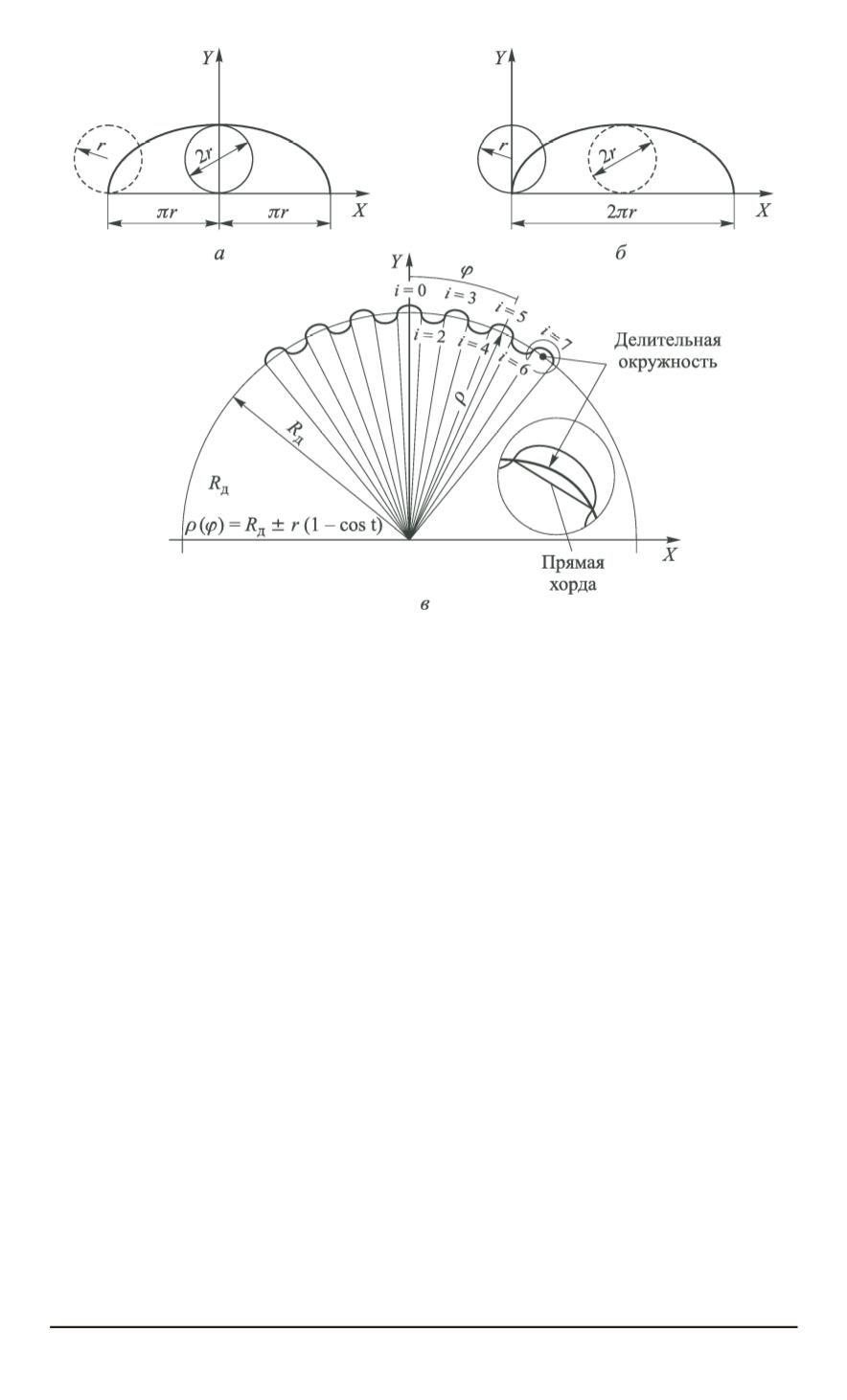
Для исследования условий взаимного расположения зубьев колес,
зазоров между ними и выявления координат точек их возможного кон-
такта целесообразно перейти к новой локальной, симметричной отно-
сительно оси
Y
системе координат, сместив эту ось вдоль оси
X
на
π
(рисунок,
б
). При этом новая форма записи функций, описывающих
смещенные арки циклоид, примет вид:
x
=
r
(
t
−
π
−
sin
t
);
(3)
y
= (+
/
−
)
r
(1
−
cos
t
)
.
(4)
Для описания вершин зубьев в колесах с внешними зубьями в вы-
ражениях (2), (4) принимается знак “+”, а для описания впадин между
зубьями принимается знак “–”. И наоборот, для колес с внутренни-
ми зубьями для вершин зубьев в (2), (4) принимается знак “–”, а для
впадин принимается знак “+”. Переход к такой локальной системе
координат обусловлен тем, что он позволяет совместить ось нулевой
пары зубьев колес с большой осью деформирования ГК, сделав отно-
сительно этой оси симметричной всю глобальную систему отсчета для
110 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 2

















