ских напряжений и температуры:
dF
i
(
σ
11
, σ
22
, T
)=
−
hc
∞
Z
0
2
π
Z
0
π
2
Z
0
r
j
e
m
i
E
mj
ε
0
F
λ
−
ε
0
B
λ
λ
5
e
hc
λkT
−
1
+
i
0
A
λ
2
πhc
2
+
+
2
π
Z
0
π
2
Z
0
(
A
mj
ρ
00
λ
−
E
mj
τ
00
λ
)
i
0
A
λ
2
πhc
2
cos
β
1
dβ
1
dθ
1
dβdθdλdS,
(29)
где
r
j
— компоненты
j
вектора
r
,
e
m
i
— компоненты
m
вектора
e
i
,
E
mj
— компоненты единичной матрицы
E
mj
=
1 0 0
0 1 0
0 0 1
.
В формуле (29) проводится суммирование по повторяющимся ин-
дексам
m, j
= 1
,
2
,
3
.
Эффективная сила светового давления на солнечный парус.
Найдем эффективную силу и эффективный момент от светового да-
вления, действующего на солнечный парус в установившемся режи-
ме. Свяжем с солнечным парусом глобальную систему координат, за-
данную направляющими векторами
e
0
1
,
e
0
2
,
e
0
3
, и рассмотрим уста-
новившийся режим, в котором напряженно-деформированное состоя-
ние не изменяется с течением времени. Пусть форма деформирован-
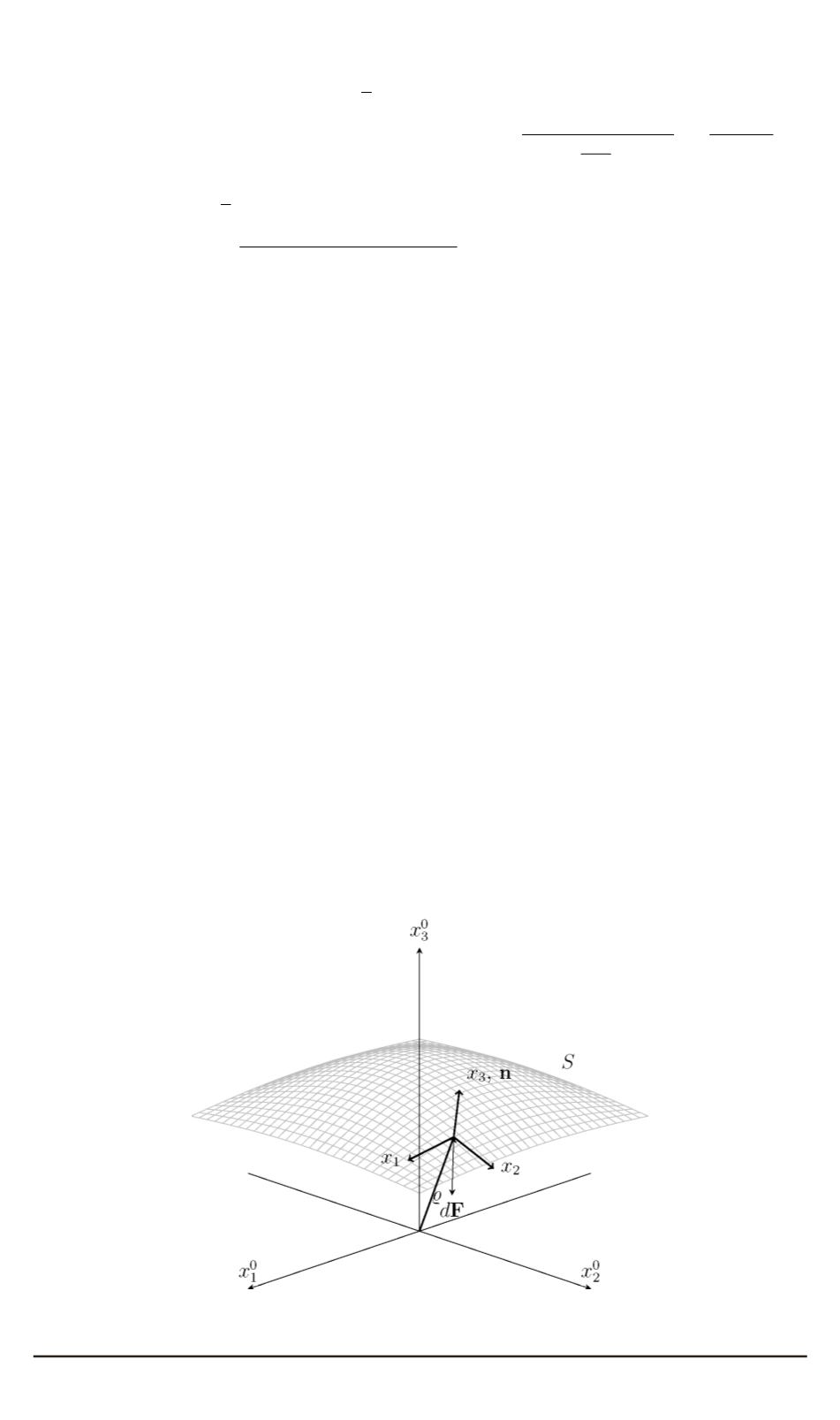
ной поверхности солнечного паруса задана следующей зависимостью
(рис. 5):
x
0
3
=
−
Φ(
x
0
1
, x
0
2
, σ
11
, σ
22
)
.
(30)
Рис. 5. Деформированная форма поверхности солнечного паруса
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 3 73


