Уравнение Навье–Стокса преобразуется в уравнение движения за-
вихренности по траекториям векторного поля
~v
+
~W
:
∂ ~
Ω
∂t
=
rot
~v
+
~W
×
~
Ω
,
(1)
где
~W
=
−
ν
r
Ω
Ω
— диффузионная скорость [8].
Граничное условие на профиле обеспечивается генерацией завих-
ренности [8]:
d
dt
Ω (
~r
K
, t
) =
J
t
(
~r
K
, t
)
,
(2)
где
J
t
— поток завихренности.
Уравнение динамики упругой оси имеет вид
u
(
s, t
) =
−
b
Z
0
G
(
s, ξ, t
)
ρ
∂
2
u
∂t
2
+
q
(
ξ, t
)
dξ,
(3)
где
G
(
s, ξ, t
)
— функция Грина для балки на податливых опорах, ко-
торая вычислена аналитически с использованием степенных поли-
номов [7] (функция нестационарная, поскольку положение пружины
s
2
=
l
(
t
))
;
q
(
s, t
)
— поперечная нагрузка на упругую ось профиля,
полученная путем интегрирования давления по части профиля
b
, на-
ходящейся в потоке среды. Распределение давления находится с ис-
пользованием аналога интеграла Коши–Лагранжа [8].
Метод решения.
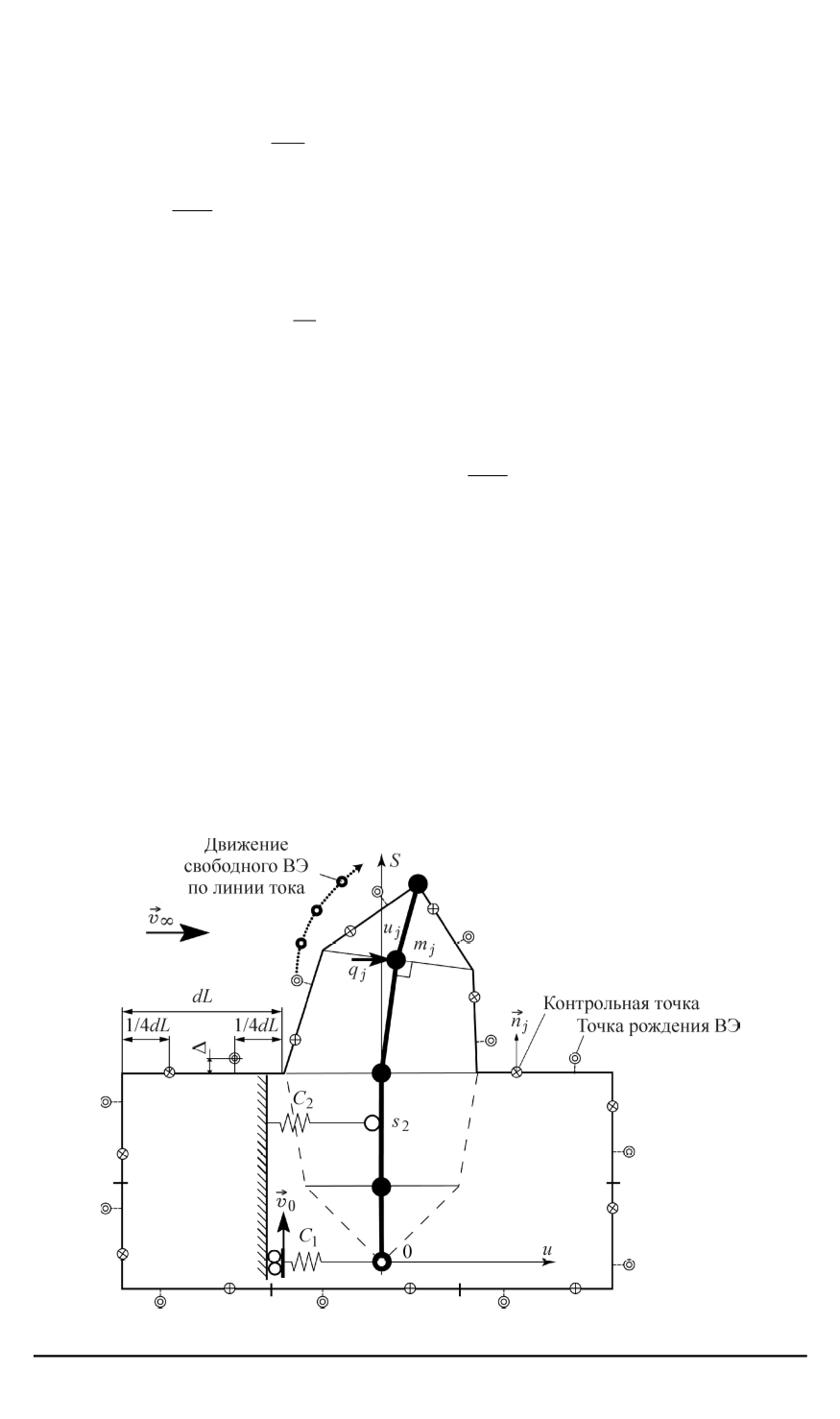
Уравнение (1) решается численно, для этого про-
водится дискретизация, как показано на рис. 2. Упругая ось балки раз-
Рис. 2. Дискретизация расчетной схемы
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 4 51


