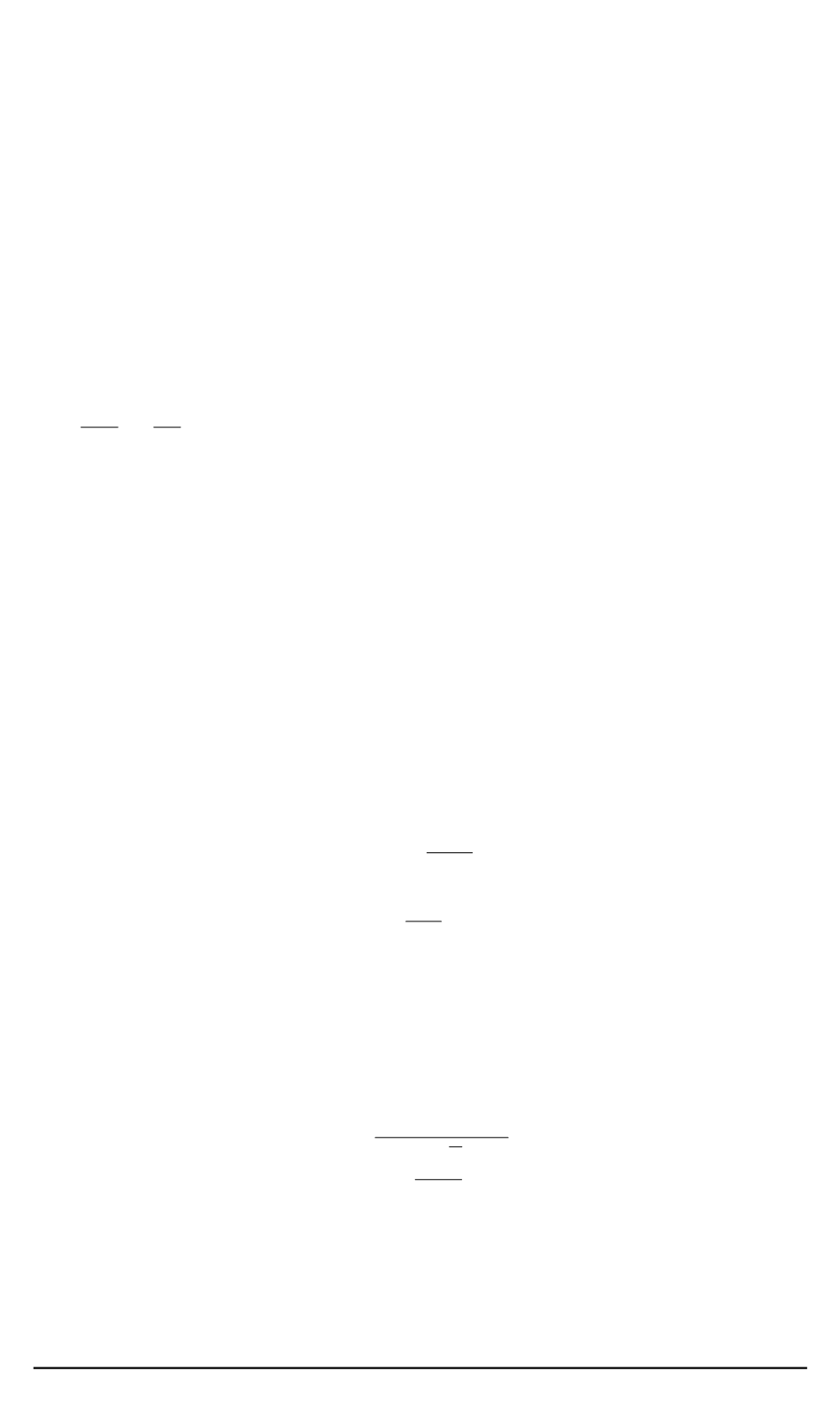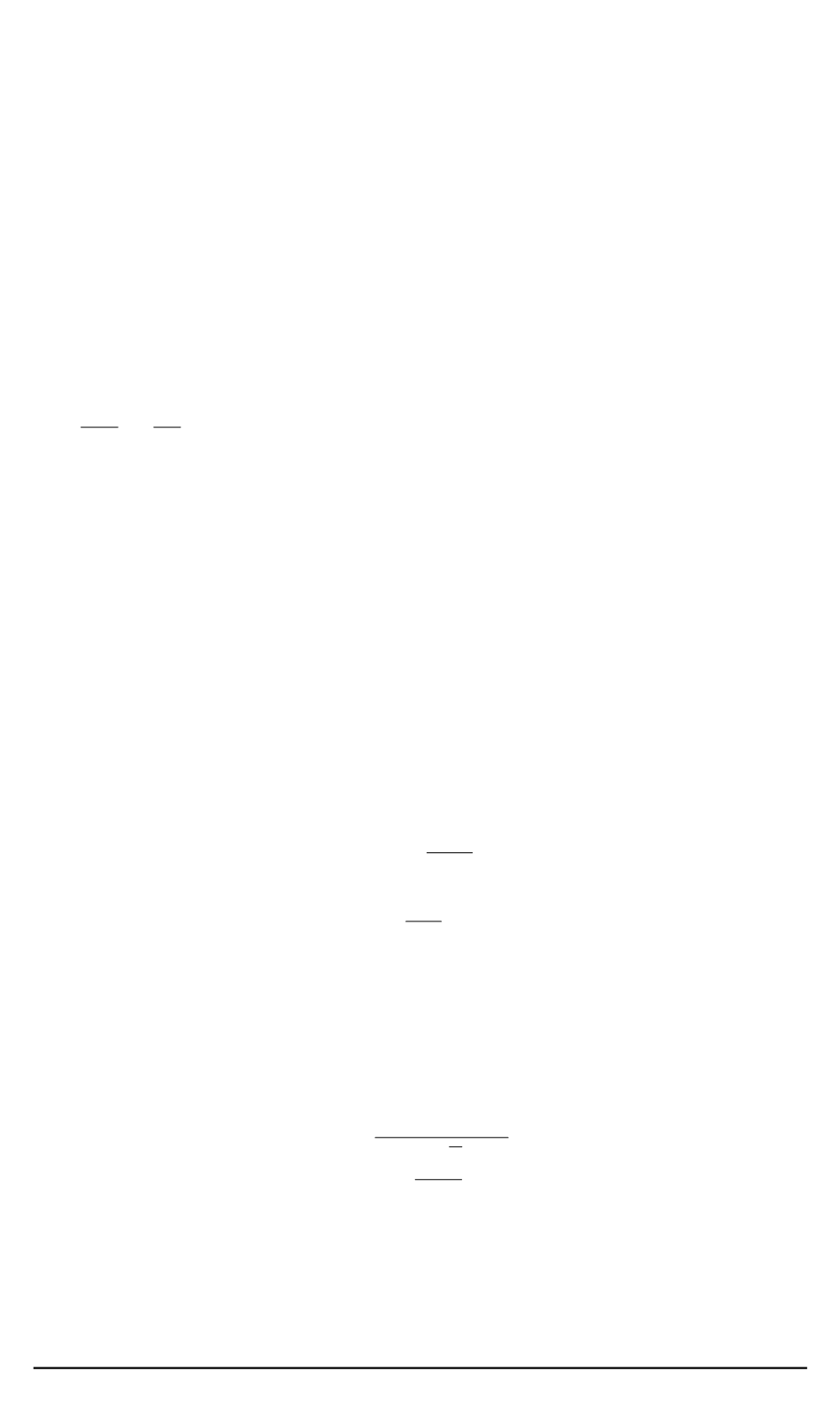
ются следующими выражениями:
F
0
=
−
4
a/
2
Z
0
p
0
(
l
)
dl
+ sin 30
◦
3
a/
2
Z
a/
2
p
0
(
l
)
dl
;
F
1
=
−
4
a/
2
Z
0
p
1
(
l
)
dl
+ sin 30
◦
3
a/
2
Z
a/
2
p
1
(
l
)
dl
.
Полученные нагрузки на единицу длины пучка формально можно рас-
сматривать как динамическую и вязкую реакции на движение, т.е.
m
0
d
2
δ
dτ
2
+
ς
dδ
dτ
=
−
(
F
0
cos
ωτ
+
F
1
sin
ωτ
) =
−
Re
(
F
0
−
iF
1
)
e
iωτ
,
(10)
где
m
0
— удельная (на единицу длины) присоединенная масса, кг/м;
ς
— удельный (на единицу длины) коэффициент диссипации, Н
∙
с/м
2
;
Re – обозначение действительной части. Общий знак минус в пра-
вой части уравнения (10) объясняется тем, что
F
0
и
F
1
представляют
собой не внешние силы, а реакции жидкости, т.е., чтобы возбудить
рассматриваемое движение жидкости, нужно приложить внешние си-
лы обратного направления.
В связи с линейностью задачи гармонические колебания могут
быть представлены в комплексном виде как
δ
(
τ
) =
Re
Ae
iωt
.
(11)
Из уравнений (10) и (11) следует
m
0
=
F
0
Aω
2
;
ς
=
F
1
Aω
.
В результате расчета получены распределения по ширине зазора дей-
ствительной и мнимой составляющих скорости по отношению к сред-
нерасходной скорости в зазоре (рис. 6).
Отношение присоединенной массы к массе, вытесненной шести-
гранником жидкости, дает коэффициент присоединенной массы
α
=
m
0
ρ
3
√
3
2
a
2
!
.
При численных решениях задач гидродинамики с малой вязкостью
возникают проблемы при определении разности близких по значени-
ям больших чисел, которые тем более существенны, чем меньше вяз-
кость
μ
или выше частота
ω
. Для преодоления указанных трудностей
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3 81