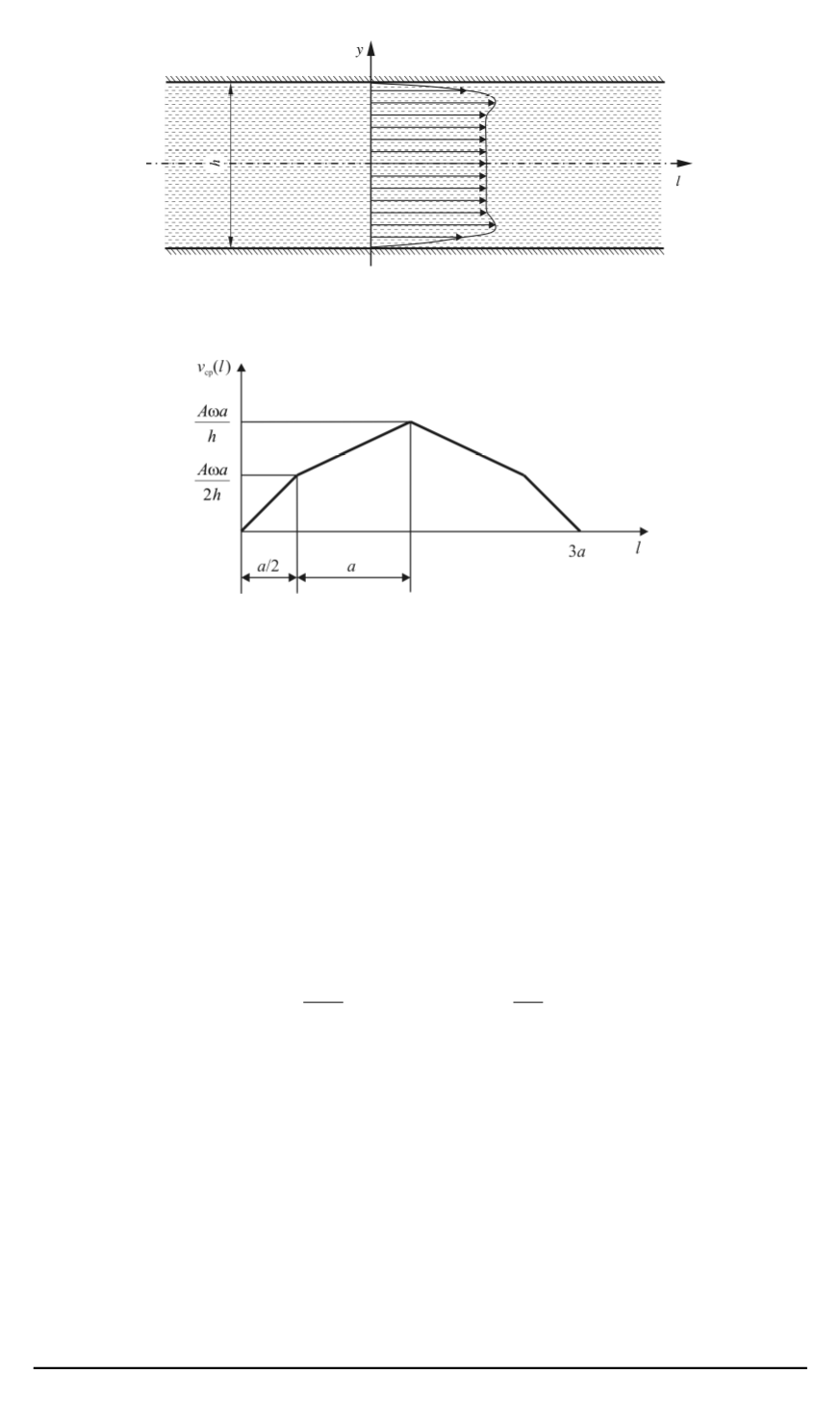
Рис. 4. Распределение продольной скорости теплоносителя по ширине шести-
гранного зазора
Рис. 5. Распределение амплитуды средней скорости потока по периметру шести-
гранного зазора
поэтому градиент скорости по ширине зазора оказывается б ´oльшим по
сравнению с продольным. В связи с этим можно пренебречь производ-
ной скорости по продольной координате (вдоль зазора) и рассматри-
вать течение в шестигранном зазоре как одномерное (рис. 4). Распреде-
ление амплитуды средней скорости по периметру зазора определяется
из условия неразрывности (рис. 5).
Уравнение движения жидкости, записанное в форме Лагранжа [2]
для перемещений жидкости
u
, и уравнение неразрывности полностью
определяют течение в шестигранном зазоре:
ρ
d
2
u
dτ
2
=
−r
p
+
μ
r
2
d
u
dτ
;
r ∙
u = 0
,
(1)
где
u
— вектор перемещений жидкости относительно неподвижной
системы координат.
Комплексное представление перемещений и давления позволяет
исключить время
u
l
= (
u
0
(
y
) +
iu
1
(
y
))
e
iωτ
;
u
y
= 0;
p
= (
p
0
(
l
) +
ip
1
(
l
))
e
iωτ
,
(2)
где
ω
— круговая частота гармонических колебаний.
78 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3


