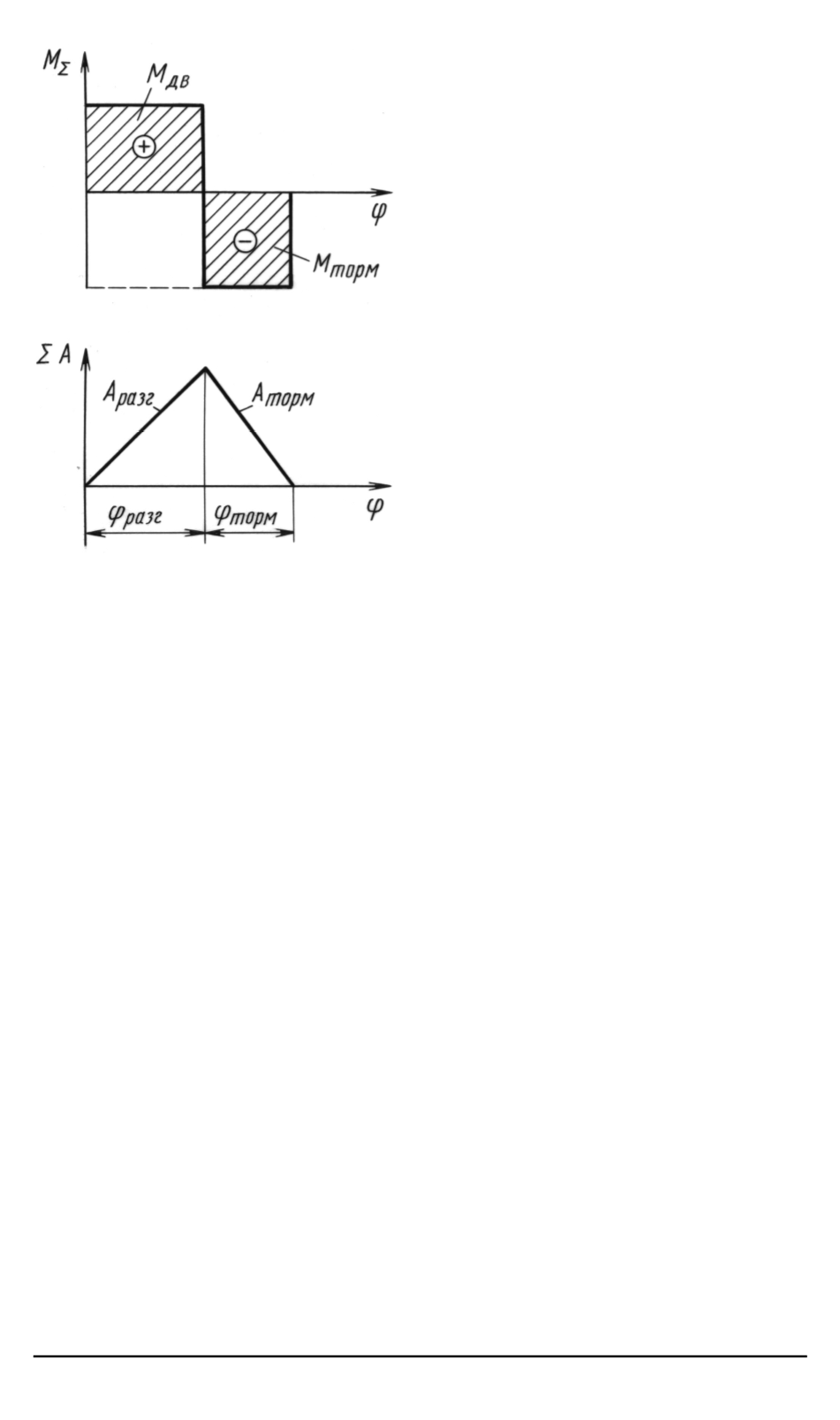
Рис. 2. Идеализированный цикл дви-
жения машинного агрегата “разгон–
торможение”
протекающих в машинах. Рассмо-
трим подробнее идеализирован-
ный неустановившийся режим, со-
стоящий из циклов разгона и сле-
дующего за ним торможения ма-
шины (рис. 2). Идеализация цикла
заключается в допущении постоян-
ства действующих моментов сил и
суммарного приведенного момента
инерции
=
Σ
[5]:
M
Σ
разг
=
M
дв
+
M
вр.сопр
+
+
M
пол.сопр
(
при разгоне
);
M
Σ
торм
=
M
торм
+
M
вр.сопр
+
+
M
пол.сопр
(
при торможении
)
,
где
М
Σ
разг
и
М
Σ
торм
— суммар-
ные приведенные моменты сил при
разгоне и торможении;
М
пол
.
сопр
и
М
вр
.
сопр
— приведенные моменты
сил полезного и вредного сопротивления;
М
торм
— момент торможе-
ния;
M
дв
— момент двигателя.
Поскольку при останове машины скорость
ω
и кинетическая энер-
гия
Т
в конце цикла равны нулю, то величина
Δ
Т
будет равна запасу
кинетической энергии в конце разгона:
Δ
Т
=
Т
mаx
=
=
Σ
ω
2
max
,
где
ω
max
— значение скорости в момент переключения машины с раз-
гона на торможение.
Суммарная работа при останове будет отрицательной, равной ра-
боте всех сил (моментов), включая полезное и вредное сопротивление:
X
A
торм
=
ϕ
торм
Z
0
M
Σ
торм
dϕ.
Модули работ при разгоне
А
разг
и останове
А
торм
должны быть равны
между собой:
A
разг
=
ϕ
разг
Z
0
M
Σ
дв
dϕ
=
A
торм
=
ϕ
торм
Z
0
M
Σ
торм
dϕ .
С учетом принятых допущений, что разгон и торможение осуще-
ствляются при постоянных значениях приведенных моментов сил и
44 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 2


