Анализ осевого вращательного движения рифленых кумулятивных облицовок

10 / 15

Анализ осевого вращательного движения рифленых кумулятивных облицовок
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 6 83
К сожалению, предложенная модель не учитывает влияние индексного угла,
поскольку не принимает во внимание влияние внутреннего рифления на пере-
распределение угловой скорости струеобразующего слоя. В связи с этим была
построена аппроксимация численной зависимости угловой скорости струеобра-
зующего слоя j  от индексного угла следующего вида:
   
1 1 1 1 ,
j A B j С     (4)
где 1 1 1, , A B C — числовые параметры;      
1 2
sin cosx x
j x
x x
  — сферическая
функция Бесселя 1-го порядка. График зависимости (4) приведен на рис. 7.
Шестой параметр — число ребер в окружном направлении n .
Экспериментальная зависимость угловой скорости струи от числа ребер n но-
сит сложный характер (см. рис. 5) [3]. Максимальное значение угловой скорости
наблюдается при числе ребер n в диапазоне от 12 до 20. С дальнейшим ростом n
компенсируемая частота меняет знак и стремится к нулю.
Зависимость угловой скорости от числа ребер n, полученная численно (рис. 8),
качественно напоминает экспериментальную (см. рис. 5). Ее максимум наблюдается
для числа ребер n = 10. С увеличением n угловая скорость меняет знак и стремится
к нулю.
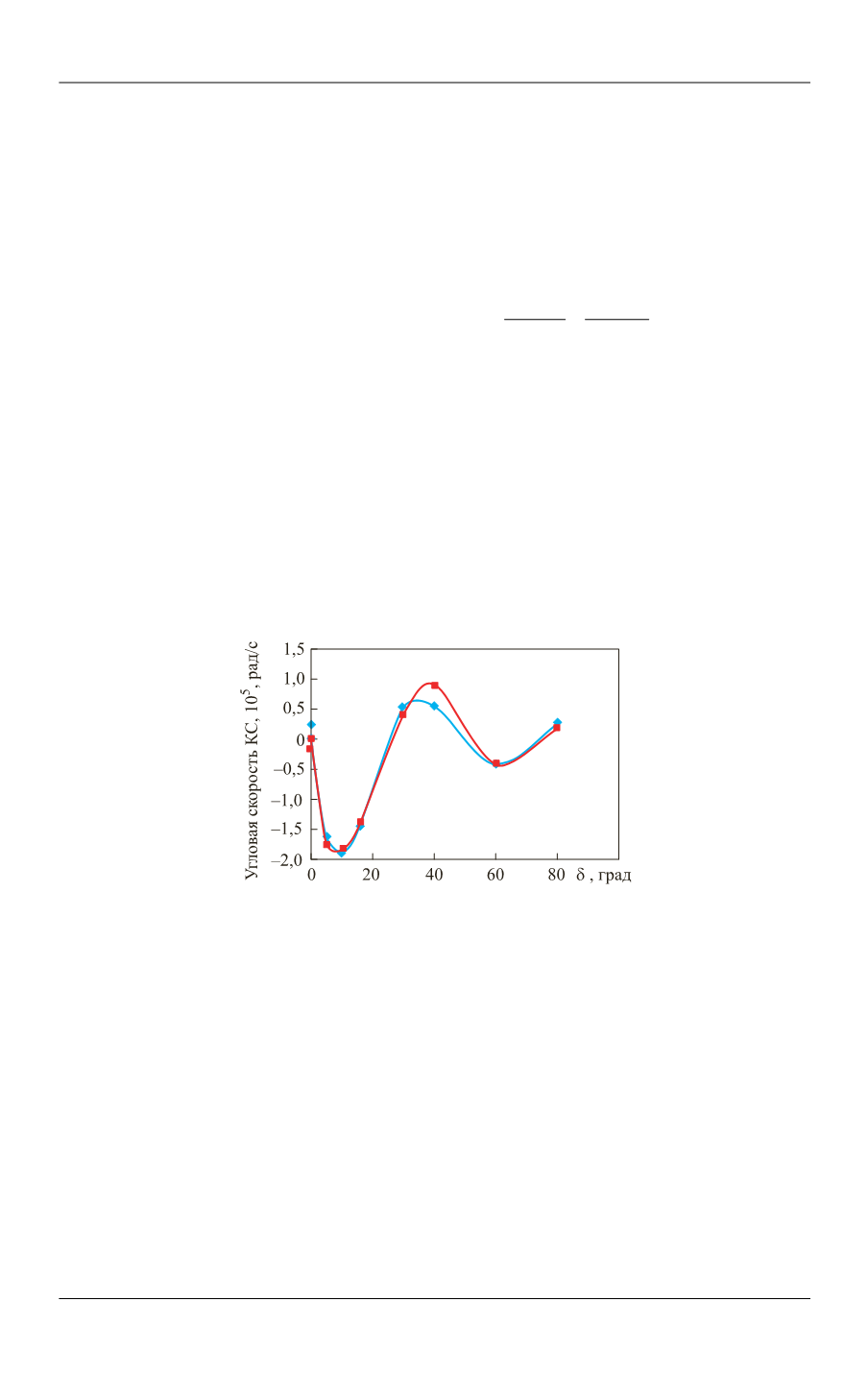
Рис. 8. Численная зависимость угловой скорости струеобразующего слоя
рифленой облицовки от числа ребер в окружном направлении
и аппроксимация этой зависимости (кривые, см. рис. 7)
Для учета влияния струеобразующего слоя на угловую скорость струи j  по
аналогии с индексным углом построена зависимость, аппроксимирующая ре-
зультаты численного расчета:
 
2 1 2 j A j B n   , (5)
где 2 2, A B — числовые параметры. График данной зависимости приведен на
рис. 8.
Другой группой параметров, определяющих закрутку струеобразующего
слоя КО, служат величины, описывающие свойства ее материала: плотность
об,  модуль Юнга Е, предел текучести ,
t  модуль упрочнения .
t E