Множественная регрессия для аэродинамическом модели беспилотных летательных аппаратов по экспериментальным данным

4 / 9

В.В. Корянов, К.Т. Нгуен, В.Т. Нгуен
62 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 5
4 4 ( )   и 2 2   равны 0,8038, а 2 2 ( )   и 2 2 ( )
    равны 0,4563, 2 2 ( )    и
( )
    равны –0,3622 и 2 2 ( )   и 2 2   равны 0,7756.
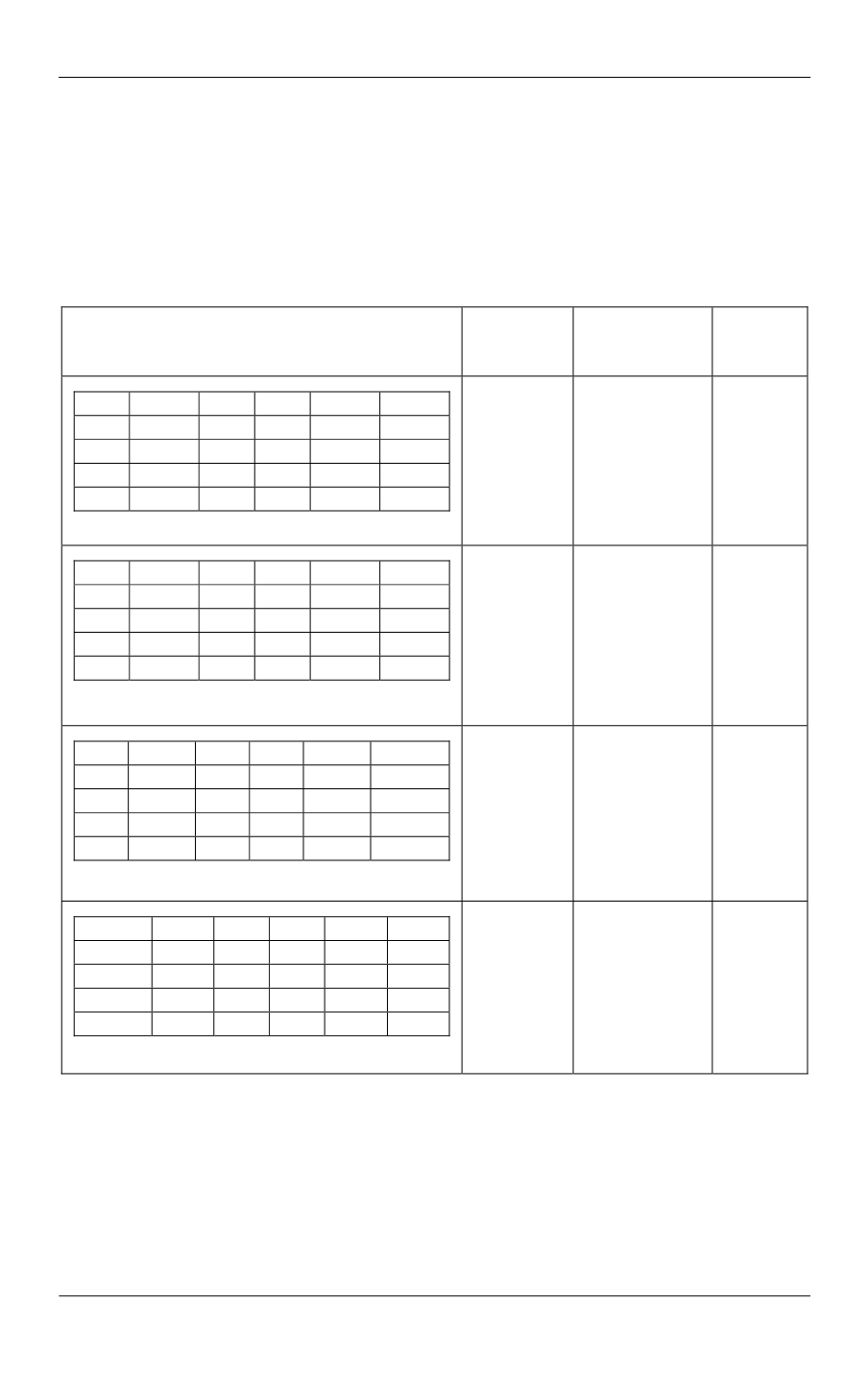
Результат расчета при использовании в качестве критерия только значения
суммы критериев регулярности приведен в табл. 2 [6]:
2 2 2 2 2
1 2 3 4 5 ( ) ( ) ( ) ( ) ( ) .
x y z y z c c c m m J B B B B B            (3)
Таблица 2
Для оценки мультиколлинеарности факторов может использоваться определитель
матрицыпарных коэффициентов корреляциимеждуфакторами [7].
Если бы факторы не коррелировали между собой, то матрица парных ко-
эффициентов корреляции между факторами была бы единичной, поскольку все
недиагональные элементы i j x x r (xi ≠ xj) были бы равны нулю. Так, для включаю-
щего три объясняющих переменных уравнения
Значения матрицы аэродинамических
коэффициентов
Значения
факторов
Критерии
оптимизации
Расчет-
ный кри-
терий
0,029 0,029 0,002 0,002 0,002 0,002
11,419 0,002 0,002 0,002 –10,134 0,002
0,002 11,419 0,002 0,002 0,002 10,134
6,537 0,002 0,002 0,002 –3,123 0,002
0,002 6,537 0,002 0,002 0,002 3,123
9948; 114
1,3; 0,5
…
9500; 114
2,8; 2,0
2
2
2
2
2
пр
( ) 17,30
( ) 181,50
( ) 683,10
( ) 5,20
( ) 2,60
= 0,45
= 0,98
x
y
z
y
z
c
c
c
m
m
P
 
 
 
 
 

1,0438
0,037 0,031 0,002 0,002 0,003 0,002
10,198 0,001 0,002 0,002 –11,134 0,002
0,002 7,740 0,002 0,001 0,002 7,719
6,125 0,002 0,003 0,001 –4,063 0,002
0,002 7,619 0,002 0,002 0,002 3,122
10484; 139
3,0; 2,4
…
10458; 124
2,4; 0,9
2
2
2
2
2
пр
( ) 16,80
( ) 312,50
( ) 11,50
( ) 1,20
( ) 1,80
= 0,83
=1,0
x
y
z
y
z
c
c
c
m
m
P
 
 
 
 
 

0,3620
0,030 0,028 0,001 0,002 0,003 0,003
13,127 0,001 0,002 0,002 –11,009 0,001
0,002 7,330 0,004 0,001 0,001 8,988
6,535 0,002 0,003 0,001 –3,870 0,002
0,003 7,523 0,001 0,002 0,002 2,499
9592; 66
3,0; 1,8
…
9644; 12
0,5; 0,1
2
2
2
2
2
пр
( ) 16,80
( ) 404,20
( ) 13,80
( ) 1,20
( ) 2,00
= 5,34
=1,00
x
y
z
y
z
c
c
c
m
m
P
 
 
 
 
 

0,3482
0,030 0,028 0,001 0,002 0,003 0,003
13,116 0,001 0,002 0,002 –10,967 0,001
0,002 7,344 0,004 0,001 0,001 8,971
6,356 0,002 0,003 0,001 –3,892 0,002
0,003 7,528 0,001 0,002 0,002 2,510
10460; 146
0,7; 0,1
…
9644; 11
2,9; 0,6
2
2
2
2
2
пр
( ) 16,70
( ) 326,70
( ) 16,40
( ) 1,30
( ) 1,70
= 5,66
=1,00
x
y
z
y
z
c
c
c
m
m
P
 
 
 
 
 

0,3456