
где
c
1
=
s
E
(1
−
ν
)
(1 +
ν
)(1
−
2
ν
)
ρ
0
— скорость распространения волн объем-
ной деформации (скорость продольной звуковой волны);
γ
=
1
−
2
ν
1
−
ν
c
1
R
0
;
E
— модуль Юнга и
ν
— коэффициент Пуассона.
При этом радиальное перемещение выражается через
f
по формуле
U
=
−
1
c
1
1
r
df
dt
−
1
r
2
f.
(17)
Для точек, лежащих на поверхности сферической полости (
r
=
R
0
),
получим
U
=
−
1
c
1
1
R
0
df
dt
−
1
R
2
0
f.
(18)
Таким образом, уравнения (7), (14), (15), (16), (18) образуют
замкнутую систему, которую можно решить численными методами.
Результаты расчета для случая протекания через канал разряда
колебательного импульса тока
i
(
t
) =
I
m
exp(
−
δt
) sin(
ωt
)
предста-
влены на рис. 2. Расчет был проведен при следующих параметрах:
I
m
= 1 000 000
А;
δ
= 50000
с
−
1
;
ω
= 100000
с
−
1
;
E
= 2
,
8
∙
10
9
Па;
ν
= 0
,
25
;
ρ
0
= 1500
кг/м
3
;
R
0
= 0
,
04
м;
σ
=
σ
= 10
4
(Ом
∙
м)
−
1
;
P
0
= 3
,
05
∙
10
8
Па;
α
= 7
,
15
;
η
= 1
,
26
.
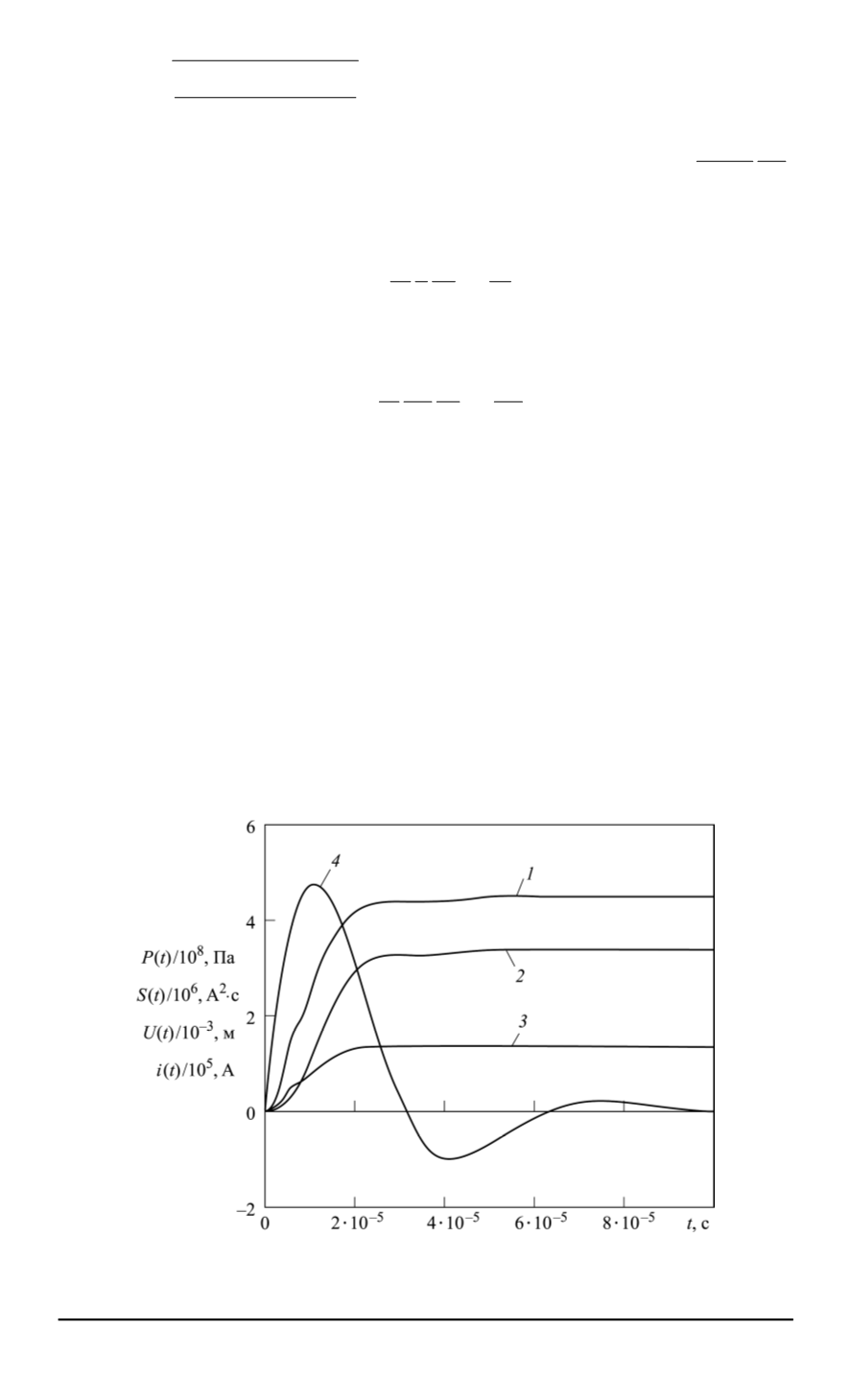
Из рис. 2 следует, что форма давления (кривая
2
) близка к сту-
пенчатой, а время нарастания до максимального значения составляет
десятки микросекунд, что лежит в характерном диапазоне электро-
гидроимпульсного эффекта (порядка 10. . . 200 мкс) и совпадает с экс-
периментальными данными.
Рис. 2. Расчетные зависимости:
1
—
S
(
t
)
;
2
—
P
(
t
)
;
3
—
U
(
t
)
;
4
—
i
(
t
)
128 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2016. № 1
















