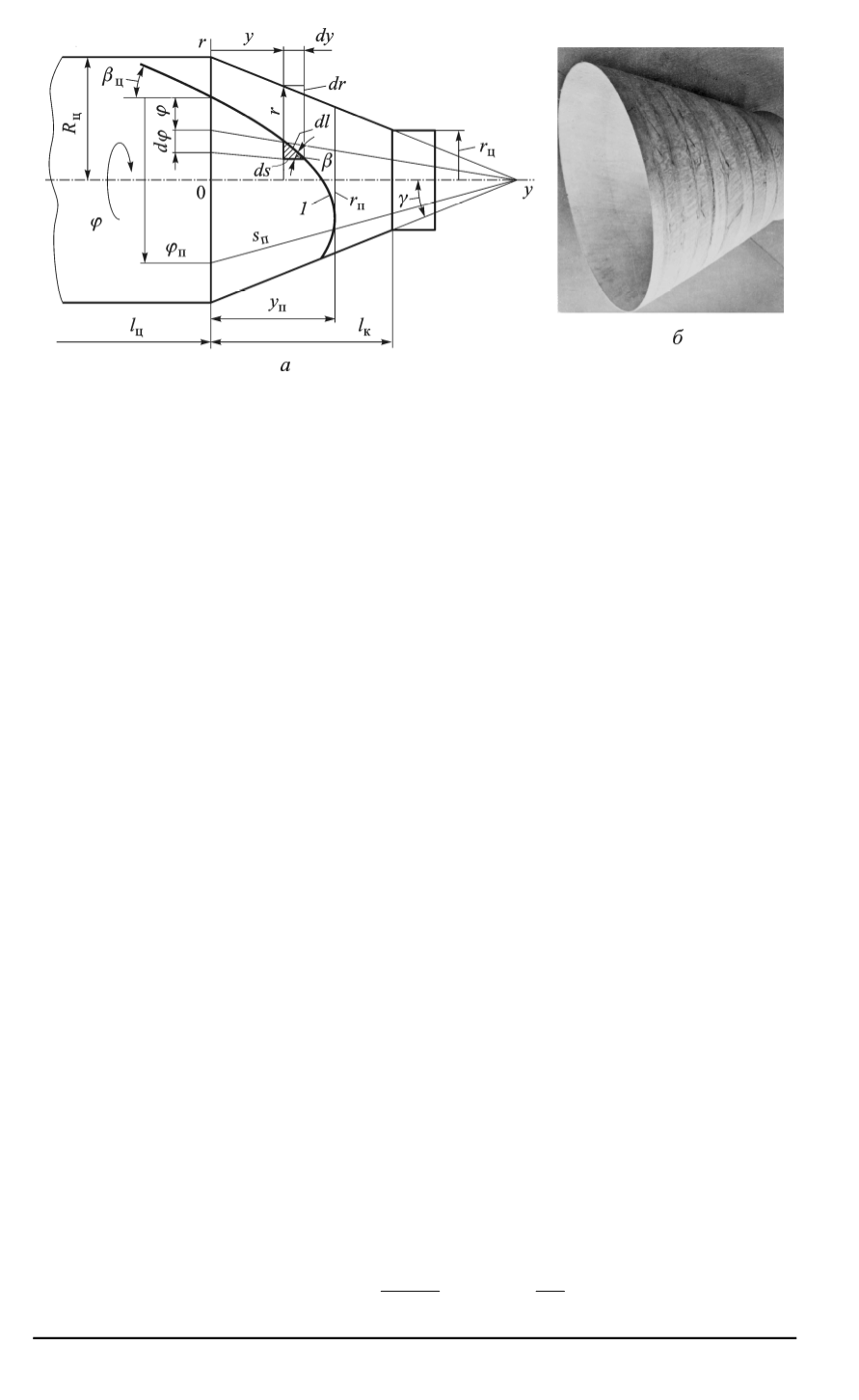
Рис. 2. Геометрия и система координат конической оболочки (
а
) и стеклопла-
стиковая коническая оболочка (
б
) (
1
— нить)
Согласно обозначениям, принятым на рис. 2,
а
, запишем основные
дифференциальные соотношения и текущие значения переменных па-
раметров для конических оболочек:
dy
=
dr/
tg
γ
;
ds
=
dr/
sin
γ
;
dl
=
dr/
(sin
γ
cos
β
r
);
dϕ
= (tg
β
r
/r
)
ds
= (tg
β
r
/
(
r
sin
γ
))
dr
;
y
= (
R
ц
−
r
)
/
tg
γ
;
s
= (
R
ц
−
r
)
/
sin
γ,
(12)
где
ds
и
dl
— элементы образующей и длины нити;
β
=
β
r
— те-
кущий угол намотки;
s
— длина образующей конической оболочки.
Кроме того, геодезические линии на поверхности оболочек вращения
определяются уравнением Клеро [2]:
r
sin
β
r
=
R
ц
sin
β
ц
=
const
.
(12а)
Когда нить касается полярного отверстия
r
=
r
п
, геометрические
размеры находят из прямоугольного треугольника, образованного ни-
тью и образующей (меридианом) на развертке конической поверхно-
сти:
y
п
=
s
п
cos
β
п
;
s
п
=
R
ц
(1
−
sin
β
ц
)
/
sin
γ
;
l
п
=
R
ц
(cos
β
ц
)
/
sin
γ
;
ϕ
п
= (
π/
2
−
β
ц
)
/
sin
γ,
(13)
где
l
п
,
s
п
,
ϕ
п
— длина нити, длина образующей и угол поворота оправки
от цилиндрической поверхности до касания нитью полярного отвер-
стия на конической поверхности.
Если намотку конической оболочки проводят по ЛРО, то для диф-
ференциального уравнения намотки
ϕ
0
r
(12), заданного на конической
поверхности (
K
1
= 0
,
K
2
= cos
γ/r
), находят геодезическую кривизну
[2] кривой
K
гд
= sin
γ
sin
β
r
r
+ cos
β
r
dβ
dr
.
(14)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2012. № 4 81


