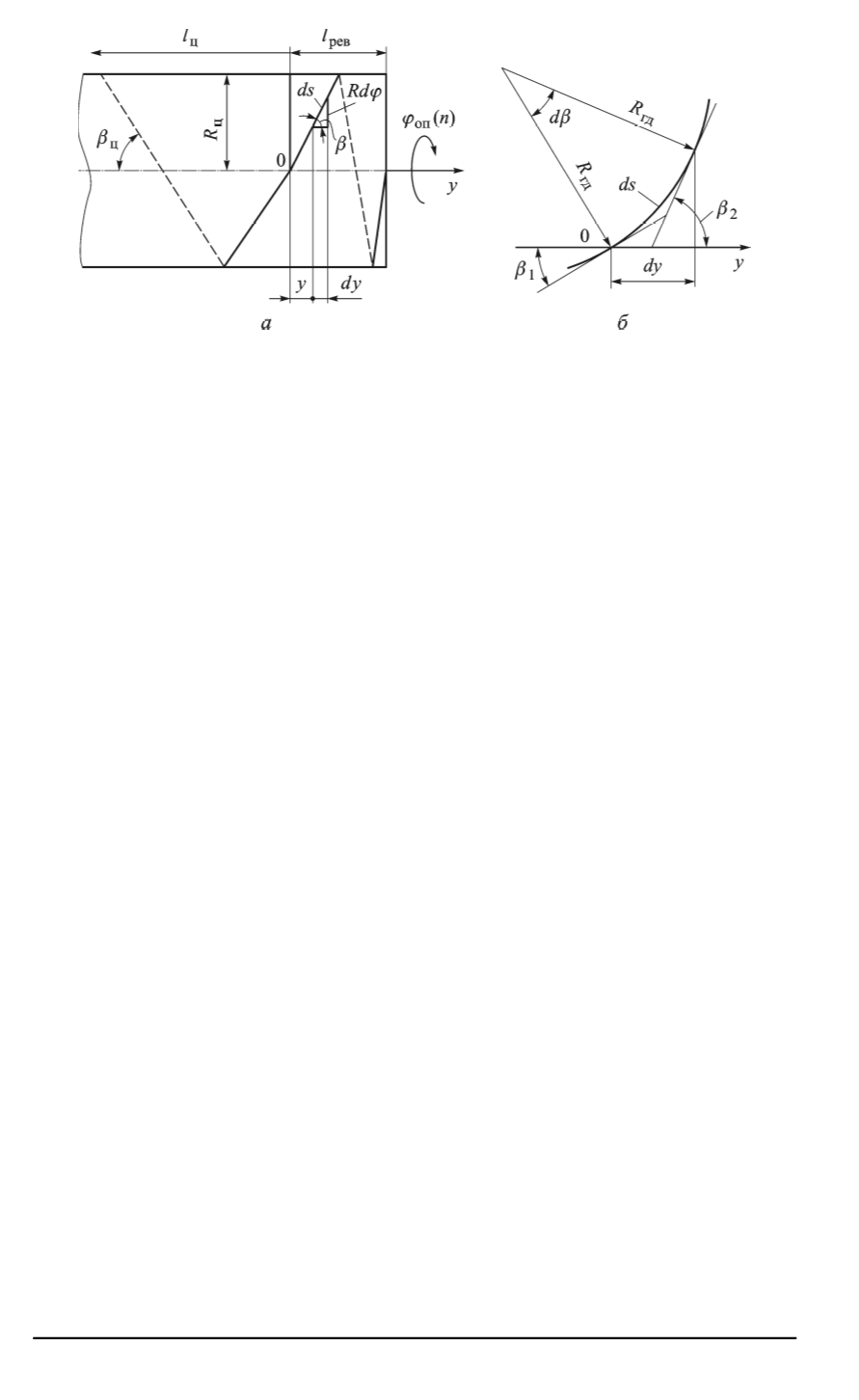
Рис. 1. Кинематика спиральной намотки с реверсом ленты на концах ци-
линдрической оболочки (
а
) и схема к определению геодезической кривизны
кривой на развертывающейся поверхности (
б
):
ϕ
оп
— угол вращение оправки (главное движение);
y
— линейное перемещение
суппорта (движение подачи);
β
— текущий угол намотки
оболочки, длины реверса
l
рев
(зоны реверса) и угла поворота оправки
ϕ
рев
в зоне реверса запишем дифференциальное соотношение
dϕ
(
y
) = tg
β
(
y
)
dy/R
ц
.
(1)
Поскольку регулярная часть длиной
l
ц
цилиндрической оболоч-
ки наматывается с постоянным углом
β
ц
=
const, то из уравне-
ния (1) находим полный угол поворота оправки на этом участке:
Φ
ц
=
l
ц
tg
β
ц
/R
ц
. На концах оболочки на длине
l
рев
намотка осу-
ществляется по ЛРО, поэтому для определения искомых величин
выразим их значения через коэффициент трения
f
тр
, равный тангенсу
угла
θ
геодезического отклонения:
tg
θ
=
K
гд
/K
n
=
R
n
/R
гд
,
(2)
где
K
n
и
K
гд
,
R
n
и
R
гд
— нормальная и геодезическая кривизна и
радиусы нормальной и геодезической кривизны кривой. Нормальную
кривизну определим из уравнения Эйлера
K
n
=
K
1
cos
2
β
+
K
2
sin
2
β.
(3)
Из уравнения (2) с учетом (3) найдем выражение радиуса гео-
дезической кривизны цилиндрической оболочки для ЛРО (
K
1
= 0
,
K
2
= 1
/R
ц
):
R
гд
tg
θ
=
R
ц
/
sin
2
β.
(4)
Для развертывающихся поверхностей радиус
R
гд
геодезической
кривизны кривой запишем из его определения (рис. 1,
б
):
R
гд
=
ds/dβ
=
dy/
(
dβ
cos
β
)
,
(5)
где
dβ
— изменение угла намотки на дуге
ds
=
dy/
cos
β
;
dβ
=
β
2
−
β
1
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2012. № 4 79


